Exercise 9BThe inverse phi-function: Ф-1In the previous exercise, we needed to find the probability that Z is less than some value, say '1.64'. To do this, we used the 'Ф' function:e.g. Find p(Z < 1.64) p(Z < 1.64) = Ф(1.64)
= 0.9495 (from tables)
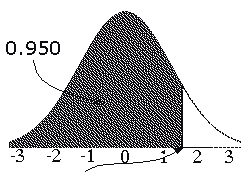
However, if we are not given the value of z, but are given the probability instead, then we need to use the inverse phi-function.e.g. p(Z < a) = 0.950. Find 'a'To sketch p(Z < a) = 0.950: p(Z < a) = 0.950 ╔══════════╝ ║ ╚═══════╗ ║ ▼ ║ ║ (1) draw a vertical ║ ║ line at Z = a ║ ▼ ║ (2) The area to the ║ LEFT of your line ║ ▼ (3) Should be 95% of the ╗ You might need to slide your area under the p.d.f. ╝ line left/right to get to ≈95%
p(Z < a) = 0.950
Ф(a) = 0.950
Ф-1 Ф-1
----------------
=> a = Ф-1(0.950)
To find Ф-1(0.950), we look up '0.950' inside the table (or the number nearest to it) and see which value of 'Z' gives this probability:
So, the answer is: 1.64Or, using the Edexcel tables to find Ф-1(0.950), we look up as close as we can find to 0.950 in the 4 digit numbers and then read across to the LEFT:
This table shows that there are two 4-digit
numbers that are equally close to 0.950, so we average them:
|
If a < 0.5: Ф-1(a) = -Ф-1(a’)
where a’ = 1 - a
|
So; to find Ф-1(0.050)
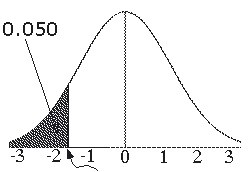
Ф-1(0.050) = -Ф-1(0.950)
= -1.65 (from tables)
For each question, sketch the
standard normal distribution,
showing the probability (area) given
Question 1: Q1 is the point on the p.d.f. where 1/4 of the data is to the left of that line:
area=¼ ║ 1 ║ ║ │ ╚══► │ │ │ │ α 0 |
To find Q1, we'd want to find 'a' if P(Z < a) = 1/4
=> Ф(α) = 0.25
Ф-1 Ф-1
----------------
α = Ф-1(0.25) ╗ Use the rule: Ф-1(a) = -Ф-1(a’)
α = -Ф-1(0.75) ◄╝ which applies when 'a' is less than 0.5
=> α = -0.67 (from tables)
Similarly, to find Q3 (let's call it 'b'),
we need the area to the right of 'b'
to be 1/4 of the whole p.d.f.
Which means the area to the left of 'b'
would be 3/4.
So, P(Z < b)
= ...
Question 2, part (a): To sketch: p(Z < a) = 0.8:
p(X < a) = 0.8 ╔══════════╝ ║ ╚════════╗ ║ ▼ ║ ║ (1) draw a vertical ║ ║ line at X = a ║ ▼ ║ (2) The area to the ║ LEFT of your line ║ ▼ (3) Should be 80% of the ╗ You might need to slide your area under the p.d.f. ╝ line left/right to get to ≈80%=> Ф(a) = 0.8 => a = Ф-1(0.8) => a = 0.84 (from table)
Question 2, part (b): p(Z < a) = 0.732 looks like this:
p(Z < a) = 0.732
╔══════════╝ ║ ╚═══════╗
║ ▼ ║
║ (1) draw a vertical ║
║ line at Z = a ║
▼ ║
(2) The area to the ║
LEFT of your line ║
▼
(3) Should be 73.2% of the ╗ You might need to slide your
area under the p.d.f. ╝ line left/right to get to ≈73%
=> Ф(a) = 0.732
Ф-1 Ф-1
-----------------
a = Ф-1(0.732)
=> a = 0.-2 (from table)
Question 2, part (c): p(Z < a) = 0.13:
=> Ф(a) = 0.13 => a = Ф-1(0.13) => a = -Ф-1(0.87) => a = -... (from table)
Question 2, part (e): p(Z > a) = 0.381 looks like this:
p(Z > a) = 0.381 ╔══════════╝ ║ ╚═══════╗ ║ ▼ ║ ║ (1) draw a vertical ║ ║ line at Z = a ║ ▼ ║ (2) The area to the ║ RIGHT of your line ║ ▼ (3) Should be 38.1% of the ╗ You might need to slide your area under the p.d.f. ╝ line left/right to get to ≈38%
area=0.381
1 │ ║
│ ║
│ ║
│ ◄╝
│
│
│
0 a
|
But, this is a RIGHT tail, and we can only do Ф-1 if we have a LEFT TAIL:
area=0.619
║ 1 │
║ │
║ │
╚► │
│
│
│
0 a
|
so p(Z < a) = 0.619
=> Ф(a) = 0.619
Ф-1 Ф-1
--------------
a = Ф-1(0.619)
=> a = ... (from tables)
Question 2, part (h): p(|Z| < a) = 0.95 is this area on the p.d.f:
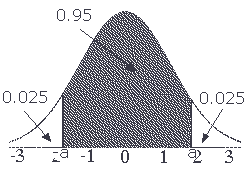
So, p(Z < a) = 0.95 + 0.025 = 0.975 ...
Question 2, part (i): This time, the sketch tells you that p(Z < a) = ...