\(\require{cancel}\)
Web Lesson #19 Trigonometry 2
› › › Multiple Solutions to Trigonometric Equations

The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!

         
  • When a question pops up, if you want to see the movie again, click ‘ 🅷🅸🅳🅴 ’ (in the top right corner)
  • You CAN'T retry a ‘flopped’ question: So 𝓟𝓐𝓨 𝓒𝓛𝓞𝓢𝓔 𝓐𝓣𝓣𝓔𝓝𝓣𝓘𝓞𝓝 and 𝓽𝓱𝓲𝓷𝓴❗
  • When you answer a question 𝒄𝒐𝒓𝒓𝒆𝒄𝒕𝒍𝒚, you'll usually get a chance to 𝐒𝐊𝐈𝐏 the explnation - but be quick!
  • Anytime you click on the © 2022 Math'scool you'll skip back to the previous section...
 
 
Trigonometry 2:

   

Multiple Solutions to Trigonometric Equations

In the animation, we learnt the origins of the graphs of \(\color{#2b83c3}{\sin \theta} \), \(\color{#62BE53}{\cos \theta}\) and \(\color{#EC7600}{\tan \theta} \)

We also learnt the the inverse trigonometric functions are formed from restricted versions of the original graphs:

 
        
        

Let's test your understanding

Question 1: The animation showed you how the \(\color{#2b83c3}{\sin \theta} \), \(\color{#62BE53}{\cos \theta}\) and \(\color{#EC7600}{\tan \theta} \) curves are formed by varying the value of \(\color{#973172}{\theta} \) this triangle:
a) Looking at the triangle and given that \(\color{#62BE53}{\cos \theta =\frac{\sqrt{5}}{3}}\), find (without using your calculator) the exact value of \(\color{#2b83c3}{\sin \theta} \)
The animation showed that \(\color{#973172}{\theta}\) can increase past 90° (at which point \(\cos \theta \) would become negative), past 180° and even past 360° (at which point the cycle would simply repeat itself)...
We also learned that the \(inv\sin \), \(inv\cos \) and \(inv\tan \) functions only use a small section of the graphs of the original functions:
b) By looking at the graphs, determine the RANGE of values that will be produced by
(i) the \(\color{#2378B4}{\sin ^{-1}}\) function,  (ii) the \(\color{#4B966E}{\cos ^{-1}}\) function and  (iii) the \(\color{#DA6610}{\tan ^{-1}}\) function
c) What would your answers to Part (b) become, if instead, \(\theta \) was measured in RADIANS

 

Hints

Part (a): I'll give you some help, in the form of a limerick:

                                   The most famous Greek, declared,
                                   a theorem that, with you, I shared,
                                   The very first rule,
                                   I taught you in Math'scool,
                                   By adding the sum of the squares!

Part (b): You can simply look at the \(\color{#973172}{\theta}\)-axis of the (restricted) graphs above; that will tell you what possible answers can be obtained when you use (say) the \(inv\sin \) button on your calculator

...then you can test your answer simply by putting lots of numbers (between \(-1\) and \(1\), obviously) into the \(\color{#2378B4}{inv\sin} \) function: i.e. \(\color{#2378B4}{\sin ^{-1}\left( -1 \right)}\), \(\color{#2378B4}{\sin ^{-1}\left( -0.7 \right)}\), \(\color{#2378B4}{\sin ^{-1}\left( -0.2 \right)}\), \(\color{#2378B4}{\sin ^{-1}\left( 0 \right)}\), \(\color{#2378B4}{\sin ^{-1}\left( 0.25 \right)}\) etc... and seeing what \(\color{#973172}{\theta}\)-values come out...

 

Question 2: Printing off this graph of part of the curve \(\color{#62BE53}{y=\cos \theta} \), you can see that a horizontal line (coloured fusia)  meets the curve at a single-point (a fusia ellipse is shown where it meets the curve)
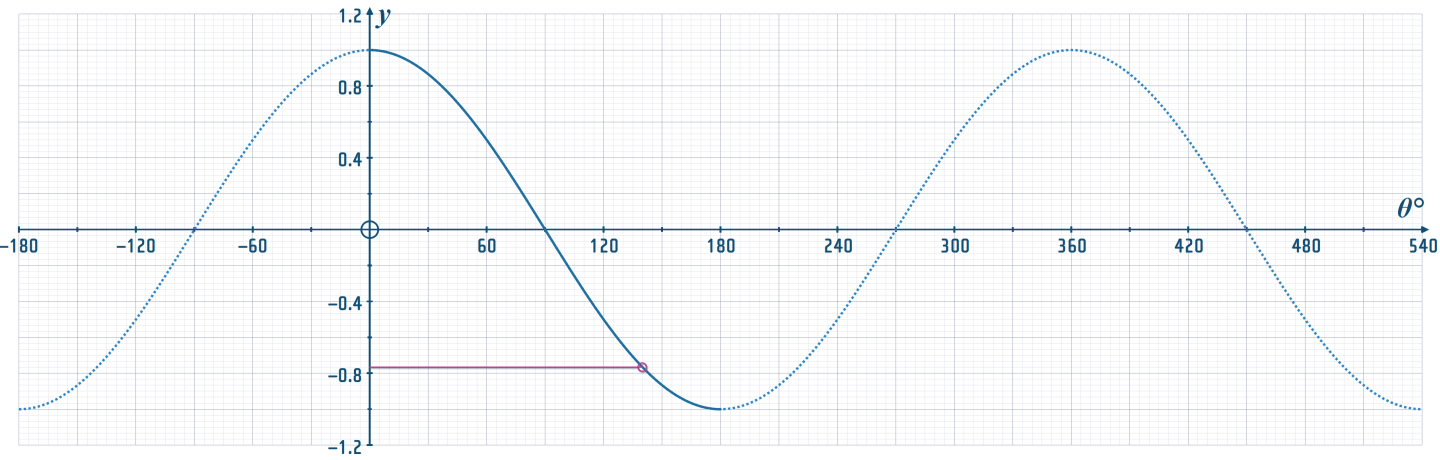
a) What is the value of \(\color{#973172}{\theta}\), where fusia coloured line meets the curve  \(\color{#62BE53}{y=\cos \theta} \) ？ (Give your answer to the nearest 5°)
b) By extending the fusia line, you can identify 3 more points on the part of the curve that is shown, that have the same \(y\)-value as the point referred to in Part (a). State the values of \(\color{#973172}{\theta}\) at those three points
c) Since you know that \(\color{#62BE53}{\cos \theta} \) has a period of 360°, state the \(\color{#973172}{\theta}\)-values of the next two points (one to the right, and one to the left) where the extended fusia line would meet the curve, beyond the interval of  \(\color{#62BE53}{y=\cos \theta} \) shown above...

 

 

Hints

Part (a): So, the first thing we can do is to draw a vertical line from the centre of the ellipse, up to the \(x\)-axis (I mean \(\theta\)-axis), then read off the \(\theta\)-value:

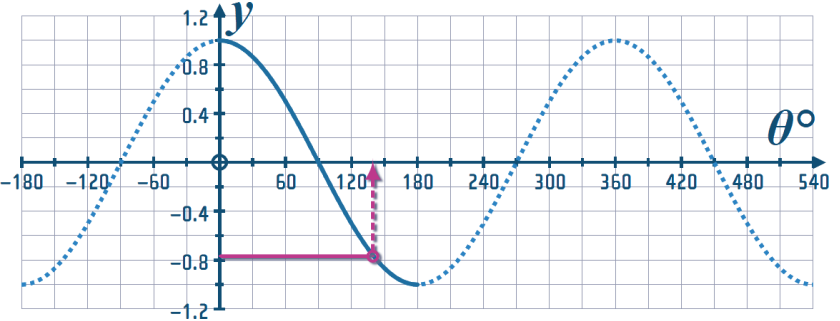
So, that's our P.V, innit ❗❓❗

 

Part (b): Extending the (fusia) horizontal line, to the until it next meets the curve:

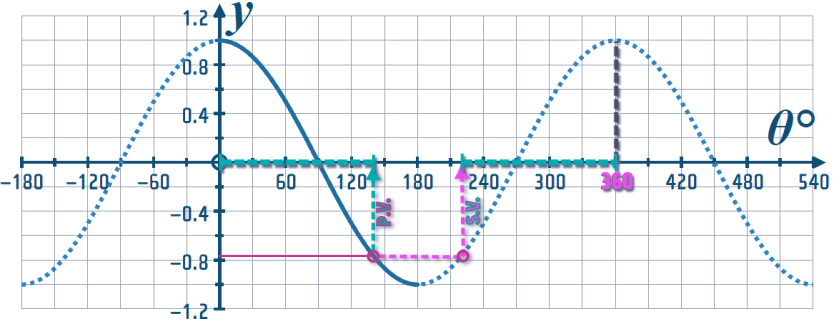
We can from the symmetry, that the horizontal GAP from \(0\) to the \(P.V.\) is symmetrically the same as the horizontal gap from \(360\) to the \(S.V.\)

So, that will allow us to pin-point the \(S.V.\)

(Of course, if we didn't have a printout of the curve in-front of us, we could revert to the RULE:  \( \text{For:}\;\cos ^{-1}\;S.V.=360°-P.V.\))

 

Part (c): Extending the (fusia) horizontal line both to the left and to the right, we find two more points where it meets the curve:

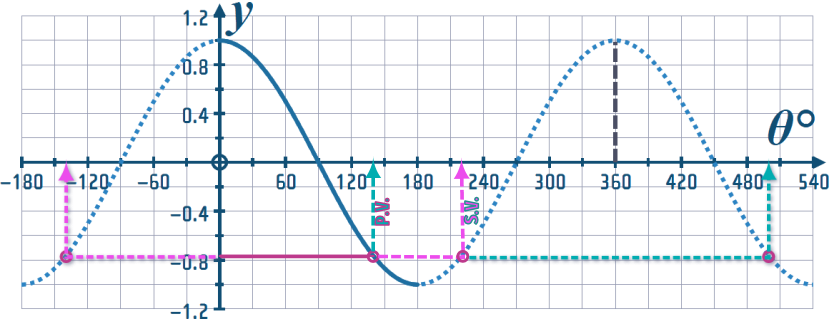
Because we know the \(\cos \theta \)  curve has a period of 360°, we can pin-point the \(\theta\) values of these points:

 

 

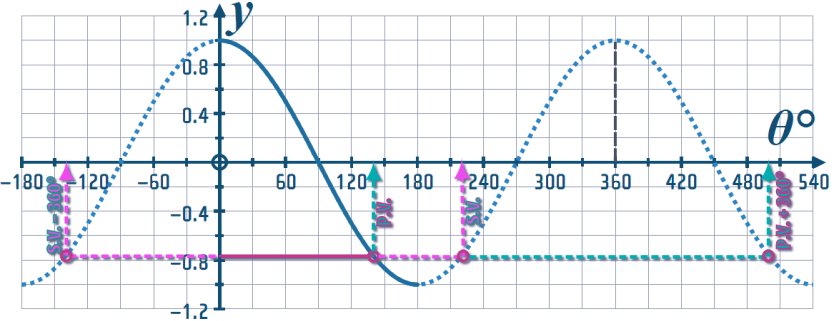
Question 3: Printing off this graph of \(\color{#EC7600}{y=\tan \theta} \), you can see that a horizontal line meets the curve:

a) What is the value of \(\color{#973172}{\theta}\), where fusia line meets the curve  \(\color{#EC7600}{y=\tan \theta}\) ？ (Give your answer to the nearest 5°)
b) By extending the fusia line, identify 3 more points on the curve that have the same \(y\)-value. State the values of \(\color{#973172}{\theta}\) at those three points
c) State the \(\color{#973172}{\theta}\)-values of the next two points (one to the right, and one to the left) where the extended fusia line would meet the curve, beyond the interval of  \(\color{#EC7600}{y=\tan \theta}\) shown...

 

 

Hints

Sorry mate - I got things to do, places to go, people to meet - you carry on!

 

Question 4:  Given \(\cos \theta =\frac{1}{4}\left( 1+\sqrt{5} \right) \):
a) Use the calculator in degrees mode to find the P.V. of \(\theta\)
b) Use the appropriate rule to find the S.V. of \(\theta\)
It is desired to find all values of \(\theta\) within the interval \(0\leqslant \theta <360\) that satisfy the equation \(\cos \theta =\frac{1}{4}\left( 1+\sqrt{5} \right) \)
c) State ('YES' or 'NO') whether adding/subtracting 360° to the P.V. or to the S.V. yields any further solutions within the interval \(0\leqslant \theta <360\)

 

Hints

	
           cos θ  =  ¼(1 + √5) 
           cos-1      cos-1 
           ---------------------
               θ  =  ……° (P.V.)
                    └─┬─┘
                      └──────────┐
                  ┌──────────────┴──────────────┐
                  │ For sin-1: S.V. = 180 - P.V.	│
                  │ For cos-1: S.V. = 360 - P.V.	│
                  │ For tan-1: S.V. = 180 + P.V.	│
                  └──────────────┬──────────────┘
                               ┌─┘
                             ┌─┴─┐
               θ  =  ……°(P.V.),	……°(S.V.)                 

Adding/ subtracting 360° does*/doesn't* produce any more solutions within the interval \(0\leqslant \theta <360\)...

*Delete as appropriate

 

 

Question 5:  Given \(\sin x=-\frac{14}{43}\):
a) Use the calculator in degrees mode to find the P.V. of \(x\) - give your answer to 1 d.p.
b) Use the appropriate rule to find the S.V.  of \(x\) (again, to 1 d.p.)
It is desired to find all of the values of \(x\) within the interval \(0\leqslant x <360\) that satisfy the equation \(\sin x=-\frac{14}{43}\)
c) State ('YES' or 'NO') whether adding/subtracting 360° to either the P.V. or the S.V. yields any further solutions within the interval \(0\leqslant x <360\)
d) Hence give all the solutions to \(\sin x=-\frac{14}{43}\) that lie within the interval \(0\leqslant x <360\)

 

Hints

		
           sin x  =  -14/43  
           sin-1      sin-1 
           ------------------
               x  =  ……° (P.V.) 
                    └─┬─┘
                      └──────────┐
                  ┌──────────────┴──────────────┐
                  │ For sin-1: S.V. = 180 - P.V.	│
                  │ For cos-1: S.V. = 360 - P.V.	│
                  │ For tan-1: S.V. = 180 + P.V.	│
                  └──────────────┬──────────────┘
                               ┌─┘
                             ┌─┴─┐
               x  =  ……°(P.V.),	……°(S.V.)                 

Adding 360° to the P.V.  does produce a solution within the interval \(0\leqslant x <360\)...

Subtracting 360° from each doesn't generate anything useful...

 

 

Question 6: Given \(\tan \alpha =2+\sqrt{3}\)
a) Use your calculator in Radians mode to find the P.V. of \(\alpha\)
b) Use the appropriate rule to find the S.V.  of \(\alpha\)
It is desired to find all of the values of \(\theta\) within the interval \(-\pi \leqslant \alpha <2\pi \) that satisfy the equation \(\tan \alpha =2+\sqrt{3}\)
c) Show that adding \(2\pi \) to either of these doesn't produce a solution within the interval  \(-\pi\leqslant \alpha <\pi \)...
                                                      ...BUT subtracting \(2\pi \) (from one of them) does produce a valid solution
d) Hence state the TWO valid solutions to \(\tan \alpha =2+\sqrt{3}\) in the interval \(-\pi\leqslant \alpha <\pi\)

 

Hints

As it says in the question, put your calculator in RADIANS mode, before typing in: \(\tan ^{-1}\left( 2+\sqrt{3} \right) \)

	
           tan α  =  2+√3   
           tan-1     tan-1 
           ---------------------
               α  =  ……° (P.V.) 
                    └─┬─┘
                      └──────────┐
                  ┌──────────────┴──────────────┐
                  │ For sin-1: S.V. =  π - P.V.	│
                  │ For cos-1: S.V. = 2π - P.V.	│
                  │ For tan-1: S.V. =  π + P.V.	│
                  └──────────────┬──────────────┘
                               ┌─┘
                             ┌─┴─┐
               α  =  ……°(P.V.),	……°(S.V.)                 

We are told that adding \(2\pi \) to these doesn't produce a valid solution, which is true, because: \(\frac{29}{12}\pi \) and \(\frac{41}{12}\pi \) are both bigger than \(2\pi\), but subtracting \(2\pi\) from the S.V. does produced a valid solution... 

 

 

Question 7: Solve \(\sin \theta =-\frac{\sqrt{2}}{2}\) finding all the answers within the interval: \(0\leqslant \theta <360\)

 

Hints

	
           sin θ  =   -½√2                           for  0 < θ < 360
           sin-1      sin-1
           ------------------
               θ  = -……°(P.V.) 
                    └─┬─┘
                      └──────────┐
                  ┌──────────────┴──────────────┐
                  │ For sin-1: S.V. = 180 - P.V.	│
                  │ For cos-1: S.V. = 360 - P.V.	│
                  │ For tan-1: S.V. = 180 + P.V.	│
                  └──────────────┬──────────────┘
                                ┌┘
                              ┌─┴─┐
               θ  = -……°(P.V.),  ……°(S.V.)  
	
 
                      ┌─────── +360 ──────┐
                      ▼                   ▼
               θ  =  -45°   ,   ……°  ,   ……°   ,   585°
                                 ▲                   ▲
                                 └────── +360 ──────┘
 
               θ  =  -45°   ,   ……  °,   ……°   ,   585°     [Eliminating unwanted answers]
	
	
So the only valid answers are: ……° and ……°

 

 

Question 8: Solve \(\sin \theta =\frac{1-\sqrt{3}}{2\sqrt{2}}\) finding all the answers within the interval: \(0\leqslant \theta <360\)

 

Hints

Hmmm, I would if I could, but I can't so I shant!

 

Question 9: Solve: \(\tan \left( 2\theta -45 \right) =-2-\sqrt{3}\) for the interval: \(0\leqslant \theta <360\)

 

Hints

In the animation, it told us that the angle in the equation, and the angle in the interval must MATCH:

	
           tan(2θ - 45) = -2-√3      ┌─────┐      interval:   0 ≤   θ   < 360
              └───┬───┘              │THESE│                       └┬┘
                  └──────────────────┤GOTTA├────────────────────────┘
                                     │MATCH│
                                     └─────┘

When they DON'T MATCH, we must MODIFY THE INTERVAL

	
           tan(2θ - 45) = -2-√3                   interval:   0 ≤   θ   < 360
              └───┬───┘                                       ×2   ×2     ×2
                  │                                           ---------------
                  │                                           0 ≤  2θ   < 720
                  │                                         -45    -45    -45
                  │                                         -----------------
                  │                                         -45 ≤ 2θ-45 < 675
                  │                                              ???????
	                └─────────────────┤ they match now!	├─────────────────┘

So, this means, once we've found the P.V. and S.V, we keep adding/subtracting 360°, right up to 675° (and down to -45°):

	
           tan(2θ - 45)  =  -2-√3                            -45 ≤ 2θ-45 < 675
           tan-1            tan-1
           ----------------------
               2θ - 45   = -75°(P.V.) 
                          └─┬─┘
                            └──────────┐
                        ┌──────────────┴──────────────┐
                        │ For sin-1: S.V. = 180 - P.V.	│
                        │ For cos-1: S.V. = 360 - P.V.	│
                        │ For tan-1: S.V. = 180 + P.V.	│
                        └──────────────┬──────────────┘
                                      ┌┘
                                     ┌┴─┐
               2θ - 45   = -75°(P.V.),  ……°(S.V.)  
	
 
                             ┌────── +360 ──────┐┌────── +360 ──────┐
                             ▼                  ▼▼                  ▼        too big
               2θ - 45   = -75°   ,   ……°   ,   ……°   ,   ……°   ,   ……°  ,   825°
                                       ▲                  ▲▲                  ▲
                                       └────── +360 ──────┘└────── +360 ──────┘

Cancelling the values that are outside of the MODIFIED-INTERVAL and then, carrying on solving:

	
               2θ - 45   = -75°   ,   ……°   ,   ……°   ,   ……°   ,   ……°  ,   825° 
                  + 45                +45       +45       +45       +45 
               --------------------------------------------------------
               2θ        =            ……°   ,   ……°   ,   ……°   ,   ……°
               ÷2                     ÷2        ÷2        ÷2        ÷2
               --------------------------------------------------------
                θ        =            ……°   ,   ……°   ,   ……°   ,   ……°

 

Question 10: Solve: \(\cos \left( \frac{3}{2}\theta +\frac{\pi}{2} \right) =\frac{1+\sqrt{5}}{4}\), finding all solutions within the interval: \(0\leqslant \theta <2\pi \)

 

Hints

It's the last and hardest question in this Web Lesson, and is your tutor here to help ❓

 

                                                                                                                                                                       😈 Like hell he is!

  

Complete this web lesson on separate paper from any other homework

The pass mark (to avoid additional homework on this topic) is:  \(\frac{8}{10}\)

        

Show FULL workings and  highlight your answers!!!