Web Lesson 15:
The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!
- When a question pops up, if you want to see the movie again, click ‘Hide’ (top right corner)
- You CAN'T retry a ‘flopped’ question: So PAY ATTENTION and THINK!
- When you get a question ‘CORRECT’, you'll get an opportunity to ‘SKIP’ the explanation:
Click the arrow in the right (but be quick!)
Transformations - Part III:
Graphs > Transformations III > Modulus Transformation
The movie shows you how to add ‘The Modulus Transformation’ to our existing suite of rules for transformations...
Whomever wrote the movie is a lazy suck-face because he didn't bother to use a flow diagram for each question - but in the hints below, I will use a FLOW DIAGRAM almost all the time the movie, they don't bother
e.g. Sketch: \(y\,=\,2 -\,\left| x^2+1 \right|\)
Rule 1:
Replace the ‘thing’ inside the brackets with: f(x)
y = 2 - │ x²+1 │
└──┬─┘
├──────────────────────┐
▼ ▼
y = 2 - │ f(x) │ f(x) = x² + 1
And call these equations (1) and (2)
y = 2 - │ f(x) │ f(x) = x² + 1
└──────────────────┘ └──────┬───────┘
equation (1) equation (2)
Rule 2:
Sketch equation (2)
f(x) = x² + 1
└──────┬───────┘
┌───────┴──────┐
│ equation (2) │
└───────┬──────┘
│
┌─────────┴─────────┐
│ start with y = x² │
│ shift up by ‘1’ │
└───────────────────┘
Rule 3:
Looking at equation (1), transform your sketch of f(x) to achieve the sketch
MODULUS outside the brackets MODULUS inside the brackets
└──────────────────┬──────────────────┘└────────────────────┬─────────────────┘
┌────────────────┴────────────────┐ ┌─────────────────┴────────────────┐
│ Reflect the bit of the curve │ │ Erase anything left of y-axis │
│ that is below the x-axis │ │ then reflect the remaining curve │
│ (in the x-axis) │ │ in the y-axis and back again │
└─────────────────────────────────┘ └──────────────────────────────────┘
┌──────────────────┐
┌──┴─┐ │
y = 2 - │ f(x) │ │
▲ ▲ ▲ ▲ ┌──────────┴──────────┐
│ │ └───┬──┘ │ you've sketched f(x)│
│ │ │ └─────────────────────┘
│ │ │
│ │ │ ┌──────────────────────────────────────┐
│ │ └──────────┤ The MODULUS is outside the brackets │
│ │ │ so reflects the bit below the x-axis │
│ │ │ (in the x-axis) │
│ │ └──────────────────────────────────────┘
│ │
│ │ ┌──────────────────────────────────────┐
│ └────────────────────┤ The NEGATIVE is outside the brackets │
│ │ so reflects the curve in the y-axis │
│ └──────────────────────────────────────┘
│
│ ┌────────────────────────────────┐
└────────────────────────────┤ The +2 is outside the brackets │
│ so shifts the curve ... by ... │
└────────────────────────────────┘
Rule 4:
Label each of the curve sections properly:
For the bit that DIDN'T get For the bit that DID get
reflected when the MODULUS reflected when the MODULUS
transformation was applied transformation was applied
└──────────────────┬─────────────────┘ └──────────────────┬─────────────────┘
┌──────────────────┴──────────────────┐ ┌───────────────────┴───────────────────┐
│ Replace the modulus with brackets │ │ Replace the modulus with -ve brackets │
│ │ │ ( ) │ │ │ │ -( ) │
└─────────────────────────────────────┘ └───────────────────────────────────────┘
For each question below, you must also state clearly the transformations you have made and label separately the line portions of the transformed curve
⋅
Question 1: Produce a detailed sketch of: \(y\,=\,\left| 2x-6 \right|\)
(a detailed sketch need to show any intercepts with the axes and any turning-points/vertices)
Clue:
Replace the ‘thing’ inside the brackets with ‘f(x)’:
y = │ 2x - 6 │
└──┬───┘
├──────────────────┐
▼ ▼
y = │ f(x) │ f(x) = 2x - 6
└──────────────┘ └───────┬─────┘
equation (1) │
┌───────┴──────┐
Start with a sketch of EQN 2: │ equation (2) │
└───────┬──────┘
│
┌───────────────┴───────────────┐
│ This is just a straight line: │
│ with y-int=-6 & grad = 2up │
│ 1across │
└───────────────────────────────┘
Now that you've sketched f(x), equation 1 tells you what other transformations you need to apply:
┌─────────────────────┐
┌──┴─┐ │
y = │ f(x) │ │
▲ ▲ ┌──────────────┴──────────────┐
└───┬──┘ │ you've already sketched f(x)│
│ └─────────────────────────────┘
│
│ ┌──────────────────────────────────────┐
└──────────────────┤ The MODULUS is outside the brackets │
│ so reflects the bit below the x-axis │
│ (in the x-axis) │
└──────────────────────────────────────┘
Now label the two curve portions; y = │ 2x - 6 │ ────────────────────┬────────────────┐
┌──────────────┴──────────────┐ │
The bit that DIDN'T get reflected: y = ( 2x - 6 ) ◄─────┤modulus changes into brackets│ │
└─────────────────────────────┘ │
┌───────────────────────────────┤
The bit the DID get reflected: y = -( 2x - 6 ) ◄─────┤modulus changes to -VE brackets│
= -2x + 6 └───────────────────────────────┘
Finally, since we are asked for a detailed sketch, we must also show any roots,
y-intercept, turning points…
Question 2: Produce a detailed sketch of: \(y\,=\,\left| x^3-8 \right|\)
Clue:
Follow the same method as in the above question…
Here's an applet for you to check - but DON'T forget to label the two portions
Question 3: Produce a detailed sketch of: \(y\,=\,\left| 1-x^2 \right|\)
Clue: Replace the ‘thing’ inside the brackets with ‘f(x)’:
y = │ 1 - x² │
└──┬───┘
├──────────────────┐
▼ ▼
y = │ f(x) │ f(x) = 1 - x²
└──────────────┘ └───────┬─────┘
equation (1) │
┌───────┴──────┐
Start with a sketch of EQN 2: │ equation (2) │
└───────┬──────┘
│
┌─────────────┴────────────┐
│ This is the curve y = x² │
│ then reflect in x-axis │
│ then shift up by ... │
└──────────────────────────┘
Now that you've sketched f(x), equation 1 tells you what other transformations you need to apply:
┌──────────────────────┐
┌──┴─┐ │
y = │ f(x) │ │
▲ ▲ ┌──────────────┴──────────────┐
└───┬──┘ │ you've already sketched f(x)│
│ └─────────────────────────────┘
│
│ ┌──────────────────────────────────────┐
└──────────────┤ The MODULUS is outside the brackets │
│ so reflects the bit below the x-axis │
│ (in the x-axis) │
└──────────────────────────────────────┘
Now label the curve portions; y = │ 1 - x² │ ────────────────────┬────────────────┐
┌──────────────┴──────────────┐ │
The bit that DIDN'T get reflected: y = ( 1 - x² ) ◄─────┤modulus changes into brackets│ │
└─────────────────────────────┘ │
┌───────────────────────────────┤
The 2 bits that DID get reflected: y = -( 1 - x² ) ◄─────┤modulus changes to -VE brackets│
= x² - 1 └───────────────────────────────┘
Now, since we are asked for a detailed sketch, we must also show any roots, y-intercept,
turning points…
Question 4: Produce a detailed sketch of: \(y\,=\,\left| \left( x+3 \right) \left( x-9 \right) \right|\)
Clue:
Remember that y = (x + 3)(x - 9) can be easily sketched (not using transformations,
but using roots and y-intercept)
Question 5: Produce a detailed sketch of: \(y\,=\,\left| \ln \left( \frac{1}{2}x \right) \right|\)
Clue: In case you've forgotten (tut tut) this is what y = ln x looks like:
Question 6: Produce a detailed sketch of: \(y\,=\,\left| 2x-6 \right|-4\)
Clue: Replace the ‘thing’ inside the brackets with ‘f(x)’:
y = │ 2x - 6 │ - 4
└──┬───┘
├──────────────────────────┐
▼ ▼
y = │ f(x) │ - 4 f(x) = 2x - 6
└──────────────────┘ └───────┬─────┘
equation (1) │
┌───────┴──────┐
Start with a sketch of EQG: │ equation (2) │
└───────┬──────┘
│
┌────────────┴────────────┐
│ This is a straight line │
│ y-int = -6; grad = 2/1 │
└─────────────────────────┘
Now that you've sketched f(x), equation 1 tells you what other transformations you need to apply:
┌──────────────────────────┐
┌──┴─┐ │
y = │ f(x) │ - 4 │
▲ ▲ ▲ ┌──────────────┴──────────────┐
└───┬──┘ │ │ you've already sketched f(x)│
│ │ └─────────────────────────────┘
│ │
│ │ ┌──────────────────────────────────────┐
└──────┼─────────┤ The MODULUS is outside the brackets │
│ │ so reflects the bit below the x-axis │
│ │ (in the x-axis) │
│ └──────────────────────────────────────┘
│
│ ┌────────────────────────────────┐
└─────────────────┤ The -4 is outside the brackets │
│ so shifts the curve ... by ... │
└────────────────────────────────┘
Question 7: Produce a detailed sketch of: \(y\,=\,\left| x^2-4x \right|+4\)
Clue:
Remember, y = x² - 4x can be sketched by factorising, using its roots and y-intercept…
Question 8: Produce a detailed sketch of: y = \(y\,=\,\,2 -\,\left| x^3-1 \right|\)
Clue:
Re-write so the term with ‘x’ is on the left:
y = 2 - │ x³ - 1 │
└┬┘└─────┬──────┘
│ ┌────┘
└──┼──────────┐
┌────┴───────┐┌─┴─┐
y = - │ x³ - 1 │ + 2
y = - │ f(x) │ + 2
Start with a sketch of: y = x³-1
Then perform the remaining transformations:
The ‘×-1’ is OUTSIDE the brackets, so it reflects the curve in the …-axis
The ‘+2’ is OUTSIDE the brackets so it shifts the curve up by ‘……’
An unknown function:
Below is a graph of \(y=f\left( x \right) \):
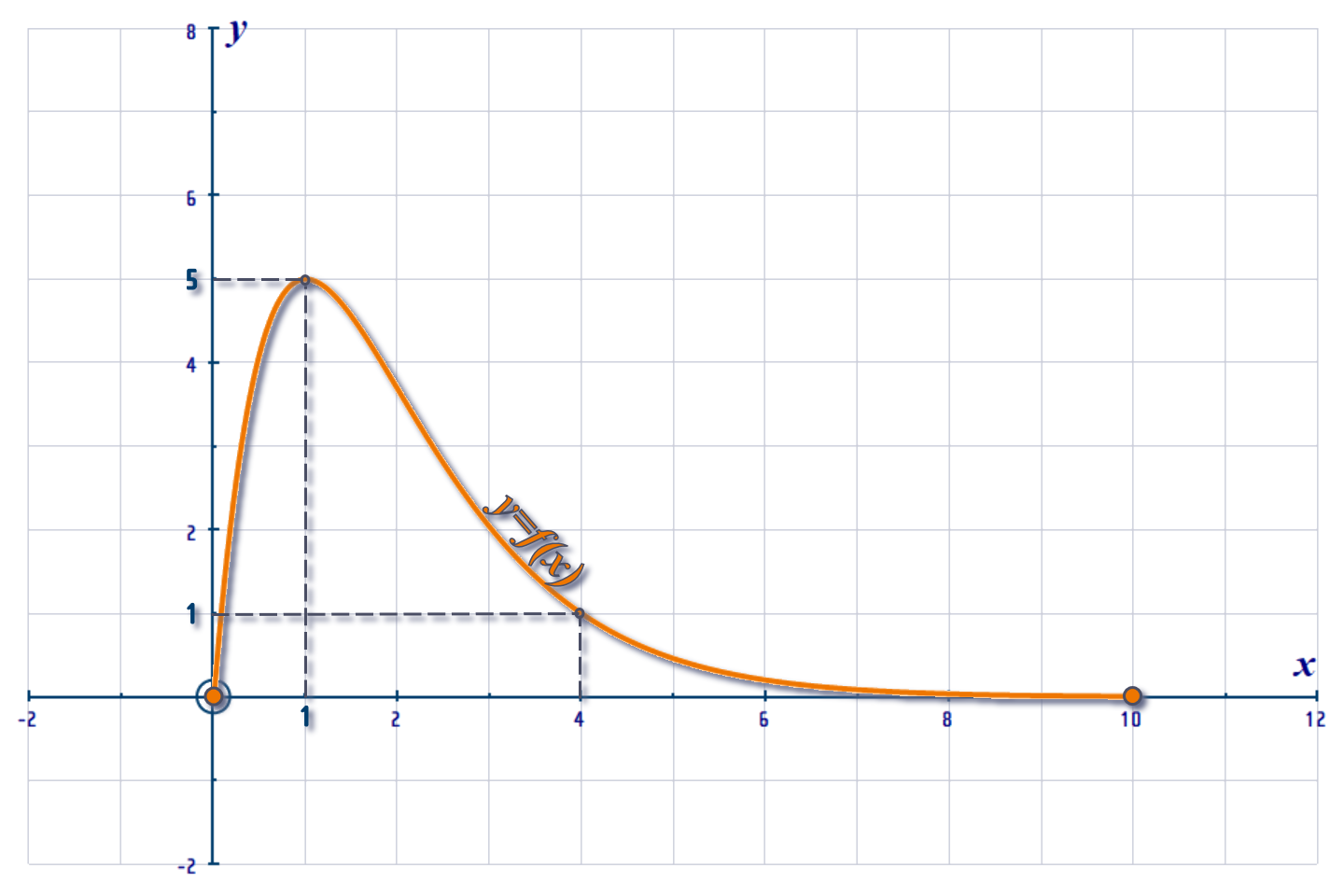
We are NOT told its equation: But we do know that \(f\left( x \right) \) is defined for \(0\leqslant x\leqslant 10\) and it has a root at \(x\,=\,0\) and another root at \(x\,=\,10\). The maximum point \(P\) is at \(\left( 1,5 \right) \).
It passes through the point \(Q\,=\,\left( 4, 1\right) \) and its gradient at \(Q\) is \(-\frac{3}{4}\)
The RANGE of \(y=f\left( x \right) \) is: \(0\leqslant yx\leqslant 5\)
Armed with this information about \(f\left( x \right) \) and the curve of \(y=f\left( x \right) \) (as shown above) and by using the same methods as in the movie, sketch the following curves.
Use squared or graph paper and use a different grid for each curve:
For each question, you must:
- State clearly the transformations you have made
- State the domain for which the transformed curve should be defined. Also state its range
- Identify the point \(P'\) (where \(P\,=\,\left( 1,5 \right) \) is on the transformed curve); and if \(P'\) is a maximum point
- Identify \(Q'\) (where \(Q\,=\,\left( 4,1 \right) \) is on the transformed curve); and state the gradient at \(Q'\)
- Identify where the points \(\left( 0,0 \right) \) and \(\left( 10,0 \right) \) have moved to; and determine if they are STILL roots
- Do you know the roots or the y-intercept of the transformed curve?
Question 9: Sketch: \(y\,\,=\,\,\left| \, f\left( x \right) -2 \right|\, \)
Clue:
I'm afraid your on your own here…
But here's an applet to keep you company!
Question 10: Sketch: \(y\,=\,3\,-\,\left| \,2\,-\,f\left( x \right) \right|\,\)
Clue:
Writing with the ‘x’ term first:
y = - │ -f(x) + 2 │ + 3
There are quite a lot of transformations do do here, so let's get them done in the right order:
Firstly:
y = - │ -f(x) + 2 │ + 3
▲ ┌─────────────────────────────────┐
└────────────┤ The +2 is outside the brackets │
│ so shifts the curve up by +2 │
└─────────────────────────────────┘
Then:
y = - │ -f(x) + 2 │ + 3
▲ ▲ ┌─────────────────────────────────────┐
└───────────┴────────────┤ The MODULUS is outside the brackets │
│ so reflects bit below the x-axis │
│ in the x-axis │
└─────────────────────────────────────┘
Next:
y = - │ -f(x) + 2 │ + 3
▲ ┌──────────────────────────────────────┐
└──────────────────────────┤ The NEGATIVE is outside the brackets │
│ so reflects the curve in the y-axis │
└──────────────────────────────────────┘
Next:
y = - │ -f(x) + 2 │ + 3
▲ ┌──────────────────────────────────────┐
└──────────────────────────────────┤ The NEGATIVE is outside the brackets │
│ so reflects the curve in the y-axis │
└──────────────────────────────────────┘
Finally:
y = - │ -f(x) + 2 │ + 3
▲ ┌────────────────────────────────┐
└─────────────────────┤ The +3 is outside the brackets │
│ so shifts the curve ... by ... │
└────────────────────────────────┘
NOTE: If you are seriously smart - I mean so smart that you annoy everyone else; you'll have realised that multiplying everything INSIDE the modulus by ‘×-1’; it actually doesn't make any difference - which leads you to a quicker route!
Complete this web lesson on separate paper from any other homework
The pass mark (to avoid additional homework on this topic) is: 8/10
Show full workings and highlight your answers
|
|

