Web Lesson 13: Transformations 1
The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!
- When a question pops up, if you want to see the movie again, click Hide (top right corner)
- You CAN'T retry a flopped question: So PAY ATTENTION and THINK!
- When you get a question CORRECT, you'll get an opportunity to SKIP the explanation:
Click the arrow in the right (but be quick!)
Transformations 1 > Translations and Reflections
Rule 1:
Makes sure the brackets are shown. Fractions often have brackets that we don't bother to show:
y = 1 should be written: y = 1
x - 2 ( x - 2 )
But, if there are no brackets, shown, then put brackets around the 'x':
y = 4 - sin x can be written as: y = 4 - sin(x)
Rule 2:
The term with 'x' in it should be the first term. If not, then swap the terms:
y = 4 - xณ can be written as: y = - xณ + 4
╘═╛╘═════╛ ╘════╛╘════╛
Rule 3:
+k INSIDE the brackets shifts the curve by -k along x
Rule 4:
A +C OUTSIDE the brackets shifts the curve by +C along y
Rule 5:
A (i.e. a negative sign, or a ื-1) OUTSIDE the brackets reflects the curve in the x-axis
Rule 6:
A (i.e. a negative sign, or a ื-1) OUTSIDE the brackets reflects the curve in the y-axis
In addition to the y = xฒ and the y = xณ curves, there are some other curves that you should know the shapes of:
.
The Recip Curve:
Below is a graph of the \(y=\frac{1}{x}\) curve (also called the "Reciprocal Curve"):
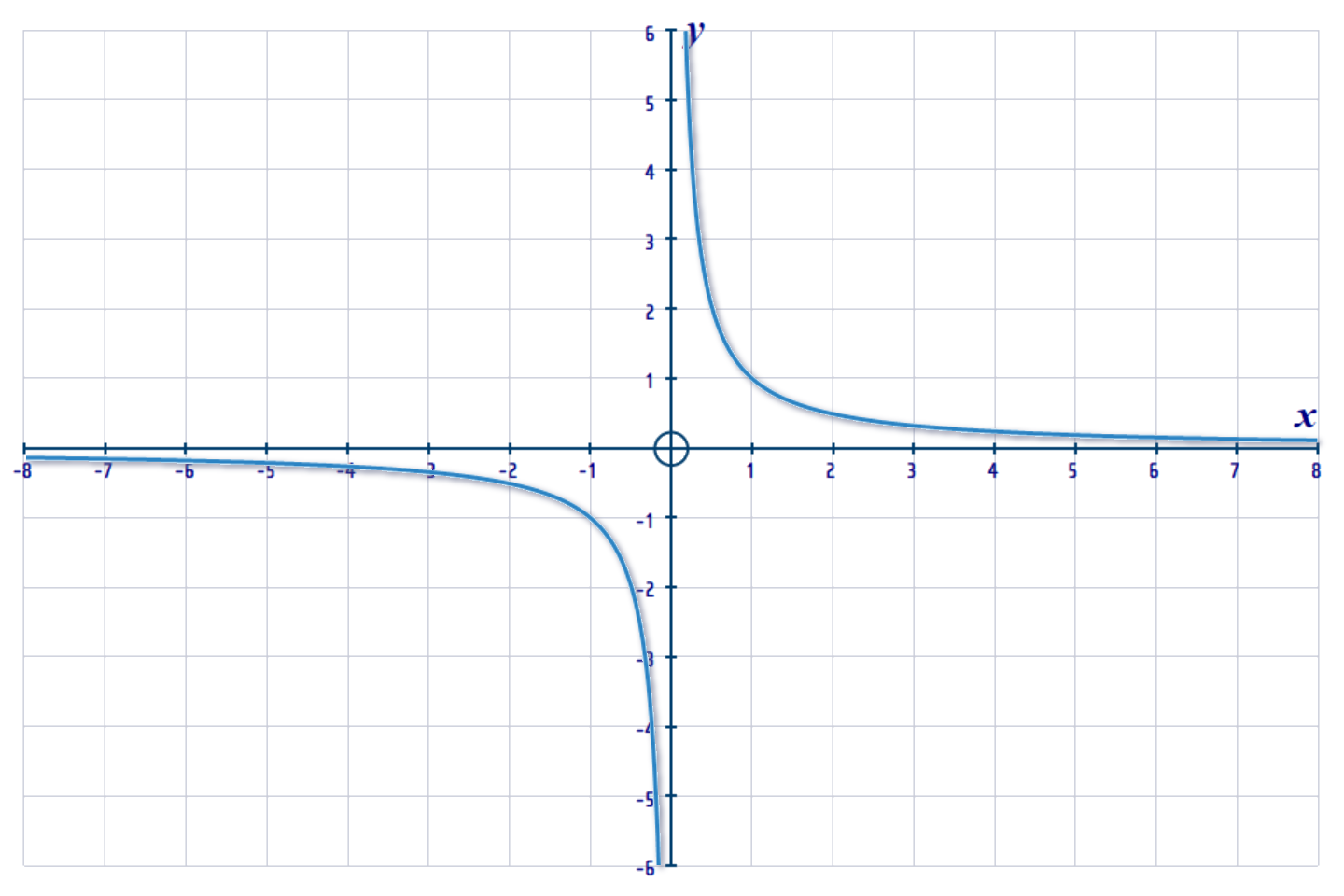
This curve has no y-intercept and it has no root, but it does have TWO ASYMPTOTES:

These are the DOTTED lines that the curve gets extremely close to, but never touches!
The horizontal asymptote is \(y\,=\,0\) (i.e. just the \(x\)-axis)
The vertical asymptote is \(x\,=\,0\) (i.e. just the \(y\)-axis)
Starting with the curve of \(y=\frac{1}{x}\) (as shown above) and by using the same methods as in the movie, sketch the following curves.
Use squared or graph paper and use a different grid for each curve:
For each question, you must:
- State clearly what transformations are needed
- Show where the asymptotes are on the transformed curve
- Identify any roots/intercepts
Question 1: Sketch: \(y\,\,=\,\,2-\frac{1}{x}\)
Clue:
In the Web Lesson, I didn't start with a flow diagram - but in these hints (and in your workings)
I wanna see a FLOW-DIAGRAM:
y = 2 - 1
▲ ▲ ( x )
└─│──────────────────────────┐
└──────────┐ │
│ │
┌─┴─┐ ┌─┴┐
x ──────────► RECIP ──────────►│ื-1│──────────►│+2│
└──┬──┘ └─┬─┘ └─┬┘
f(x) │ │
┌──────────┘ └──────────┐
┌─────┴─────────────┐ │
│ื-1 is after f(x)│ │
│ REFLECT IN x-AXIS │ ┌──────────────┴───────┐
└───────────────────┘ │ +2 is after f(x) │
│ TRANSLATE ⍰ along y │
└──────────────────────┘
After you've sketched the transformed curve, don't forget to show the new asymptotes
and the new x-intercept (root)
Question 2: Sketch: \(y\,\,=\,\,-\frac{1}{x+3}\)
Clue:
Since there is a 'sum' in the denominator, there should be brackets around the denominator:
y = 1
▲(x + 3)
│ ▲
└───│────────────────────────┐
┌────────┘ │
│ │
┌─┴┐ ┌─┴─┐
x ──────────►│+3│───────────► RECIP ──────────►│ื-1│
└─┬┘ └──┬──┘ └─┬─┘
│ f(x) │
└──┐ └──────┐
┌──────┴───────────────┐ │
│ +3 is before f(x): │ │
│TRANSLATE -3 ALONG x│ ┌─────────────┴─────┐
└──────────────────────┘ │ื-1 is after f(x)│
│ REFLECT IN x-AXIS │
└───────────────────┘
After you've sketched the transformed curve, don't forget to show the new asymptotes
and the new y-intercept
Question 3: Sketch: \(y\,\,=\,\,2-\frac{1}{x-1}\)
Clue: Since there are no brackets, first put a brackets around the x:
y = 2 - 1
(x - 1)
The FLOW DIAGRAM looks like this:
x ──────────► -1 ───────────► RECIP ──────────► ื-1 ──────────► +2
└─┬┘ └──┬──┘ └─┬─┘ └─┬┘
① f(x) ② ③
┌──────────┴──────────┐ │ │
+3 is before f(x): │ │
TRANSLATE +1 ALONG x ┌────────────┴─────┐ │
ื-1 is after f(x) │
REFLECT IN x-AXIS ┌────┴────┐
BLAH-BLAH
After you've sketched the transformed curve, don't forget to show the new asymptotes
You can use this applet to check your answers to Questions 1, 2 and 3:
Question 4: Sketch \(y=\frac{3x+13}{x+4}\)
Clue:
At first, you should think, but x appears in two places, so you can't use transformations
to sketch this
Which is true - you can only use transformations with equations where x appears only once!
But then you think, so how does he expect me to do this?
And slowly, you remember POLYNOMIAL DIVISION:
We need to re-write: (3x+13) ๗ (x+4) and polynomial division will allow us to do that:
┌─────────────
x + 4 │ 3x + 13
│ └────────────────────────────────────────────────────┐
└──────────────────────────────────────────────────┐ │
The first question we have to ask is, " what do you multiply x by, to get 3x "
The answer (obviously) is: 3
So we put a 3 on the TOP of the division and multiply it out:
┌───┌────── 3
│ │ ┌─────────────
x + 4 │ 3x + 13
Which gives:
┌───┌────── 3
│ │ ┌─────────────
x + 4 │ 3x + 13
3x + 12
Then, we subtract:
3
┌─────────────
x + 4 │ 3x + 13
│ ──(3x + 12)
│ -----------
│ 1
│ └─────────────────────────────────────────────────────────┐
└─────────────────────────────────────────────────────────────┐ │
Now, at this stage, there is NO POINT in asking, " what do you multiply x by, to get 1 "
(because you'd have to divide (not multiply) by x)
So, we STOP and re-write as:
QUOTIENT + REMAINDER
DIVISOR .
And now we've re-written it with x in 1-place, so we can use TRANSFORMATIONS to sketch it!
The Sine Curve:
Below is a graph of the \(y=\sin x\) curve (also called the "Sine Curve"):
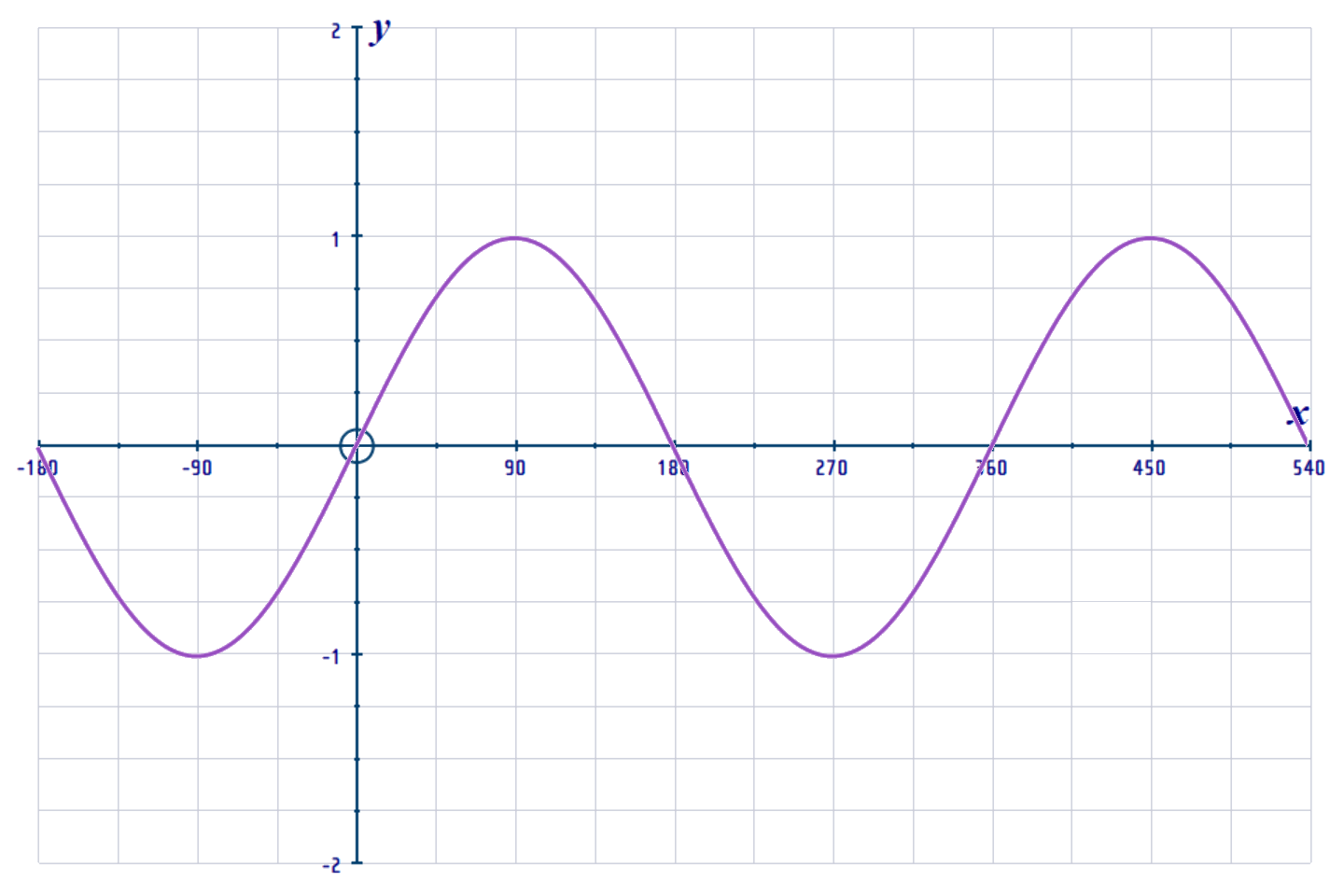
As in the WEB-LESSON, when performing TRANSFORMATIONS, but is a good idea to start with one cycle of the curve of \(y=\sin x\) (as shown below):
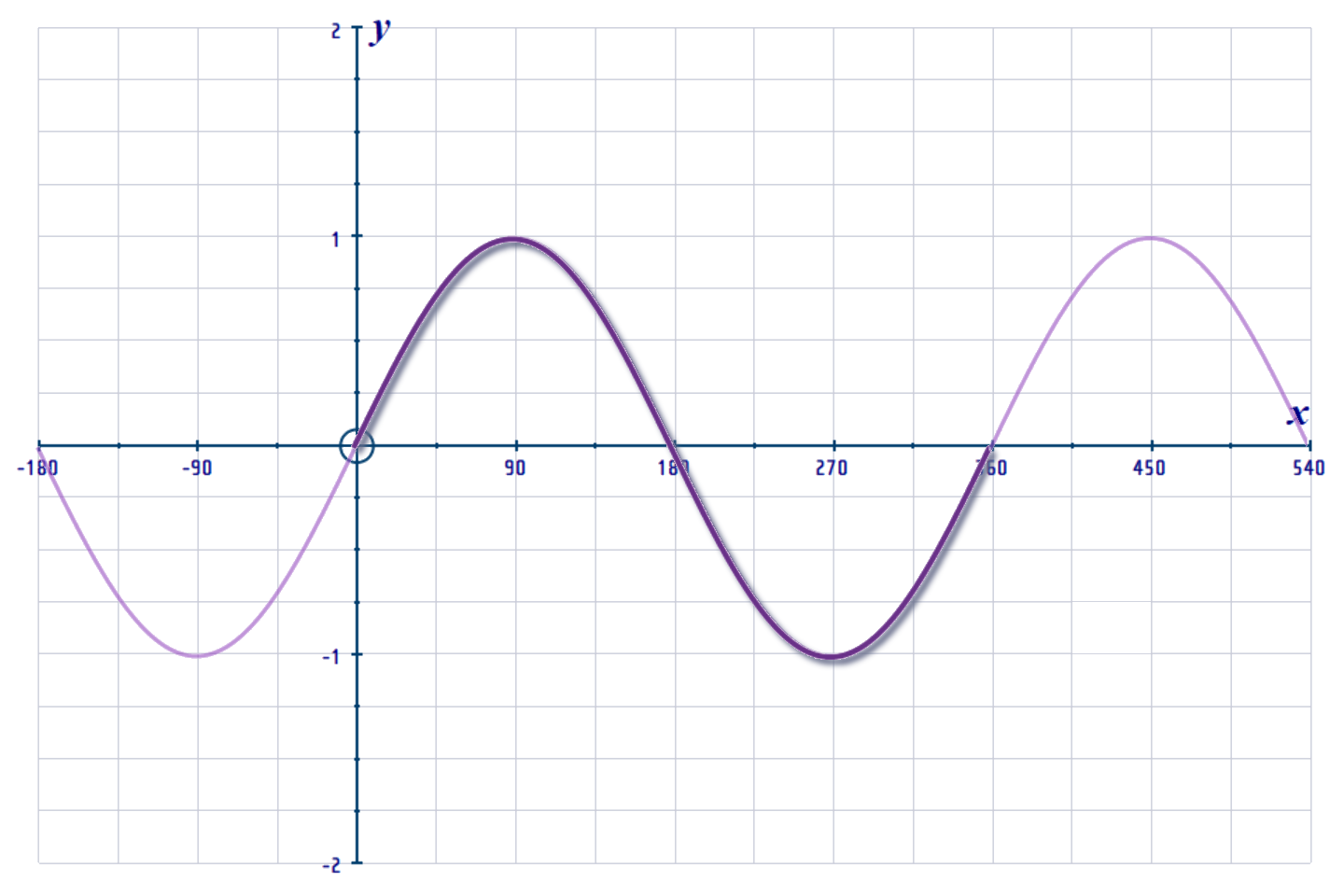
By using the same methods as in the movie, sketch the following curves. Use squared or graph paper and use a different grid for each curve:
For each question, you must:
- State clearly the transformations you have made
- Identify where the roots (0, 0), (180, 0) and (360, 0) have moved to...
- Identify where the turning points (90, 1) and (270, -1) have moved to...
[these are the bounds (highest and lowest y-values)]
Question 5: Sketch: \(y=1+\sin \left( x-30 \right) \)
Clue:
In the Web Lesson, I didn't start with a flow diagram - but in these hints (and in your workings)
I wanna see a FLOW-DIAGRAM:
y = 1 + sin(x - 30)
▲ ▲
└───────────│─────────────────┐
┌────────────────┘ │
│ │
┌─┴─┐ ┌─┴┐
x ──────────►│-30│───────────► RECIP ──────────►│+1│
└─┬─┘ └──┬──┘ └─┬┘
│ f(x) │
└──┐ └──────┐
┌──────┴────────────────┐ │
│ -30 is before f(x): │ │
│TRANSLATE -30 ALONG x│ ┌─────────────┴───────┐
└───────────────────────┘ │ +1 is after f(x) │
│TRANSLATE ⍰ ALONG y│
└─────────────────────┘
One cycle of the y = sin x graph starts at (0, 0), crosses the x-axis at (180, 0)
and ends at (360, 0); these are its ROOTS
so label where these points have moved to:
ROOTS:
y = sin x: (0, 0), (180,0) and (360, 0) ──┐
├── +30 to the x-values
y = sin(x-30): (30, 0), (⍰, 0) and (390, 0) ◄─┤
├── +1 to the y-values
y = 1+sin(x-30): (30, ⍰), (⍰, ⍰) and (390, ⍰) ◄─┘
And the TURNING POINTS:
y = sin x: (90, 1) and (270, -1) ──┐
├── +30 to the x-values
y = sin(x-30): (120, 1) and (300, -1) ◄─┤
├── +1 to the y-values
y = 1+sin(x-30): (⍰⍰, ⍰) and (300, ⍰) ─┘
So: ymax is 2 and ymin is 0 (these are called the bounds of the curve)
Question 6: Sketch: \(y=1-\sin \left( x+90 \right) \)
Clue:
Re-write so the term with x is on the left:
y = 1 - sin(x+90)
╘═╦╛╘═══╦═══════╛
║ ╔══╝
╚══╫═════════╗
╒═══╩══════╕╒═╩═╕
y = - sin(x+90) + 1
└┬┘└─┬┘ └─┬┘└─┬─┘
② f(x) ① ③
┌────────────┘ │ └──────────────┐
│ │ │
│ ┌─────────────┴──────────────┐ │
│ "+90" is INSIDE the brackets │
│ Translate by ⍰⍰ along x │
│ │
┌───────────┴─────────────────┐ │
"ื-1" is OUTSIDE the brackets │
Reflect in the x-axis ┌─────────┴───────────────────┐
"+1" is OUTSIDE the brackets
Translate the by ⍰⍰ along y
1-cycle of the y = sin x graph has roots at (0, 0), (180, 0) and (360, 0);
so label where these points have moved to:
y = sin x has turning points at: (90, 1) and (270, -1): Show where these have moved to
ymax is
and ymin is
(these are called the bounds of the curve)
Question 7: Sketch: \(y=2+\sin \left( -x+60 \right) \)
Clue:
The FLOW-DIAGRAM looks like this:
x ──────────► ื-1 ───────────► +60 ───────────► sin ──────────► +1
╘══════════╤═════════╛ └─┬─┘
│ f(x)
┌───────────────┴────────────────┐
┌──┘ You can see that there are TWO └──┐
┌──────────┤ transformations INSIDE the brackets! │
│ └──────────────────────────────────────┘
│
└───────► There is an ISSUE when we have MULTIPLE transformations INSIDE the brackets!
FOR NOW - WE WILL SIMPLY ⛔ BAN ⛔ it (later, we'll learn how to deal with it!
└────┬────┘
┌──────────────────────────┴──────────────────────────┐
│ How can you answer the question if we've BANNED it? │
└─────────────────────────────────────────────────────┘
Well -we need to go back to a simple RULE that we learnt a while back...
OKAY: We wanna RE-WRITE: 1 + sin (-x+60)
We learnt that SINE is an ODD function: f(-x) ≡ -f(x)
▲ ▲
┌───────────┘ └────────────┐
┌────────────┴───────────┐ │
┌─┘ multiplying everything └──┐ ┌──────┴──────────┐
│ inside the brackets by -1 ├───►►───┤ Is the same as: │
└─────────────────────┬───────┘ │ THROWING a -1 │
│ └─┐ in-front of ┌─┘
│ └───┐ the ┌───┘
│ │ SIN │
│ └──┬──┘
┌────┴────┐ ┌──────┴────┐
SO: sin(x-60) ≡ -sin(-x+60)
└─┬──┘ ▲
│ └──────┐
┌─────────┴─────────┐ ┌─────────┴─────────────────┐
│Here, I multiplied │ │Here, I left the INSIDE of │
│INSIDE the brackets│ │the brackets alone, but put│
└─────┐ by -1 ┌─────┘ │a -1 in-front of the SIN │
└───┬───┘ └─────────┬─────────────────┘
└─────────┐ื-1 │ื-1
┌────────────────┼───────────────┘
┌─────┴────┐ ┌────┴─────┐
Which means we can REPLACE sin(-x+60) with -sin(x-60)
Having re-written it - we can now proceed as usual!
Question 8: Sketch: \(y=2-\sin \left( -x+90 \right) \)
Clue:
Sorry, I cannae help yu - but I've put an applet for you to check your working
An unknown function:
Below is a graph of \(y=f\left( x \right) \):
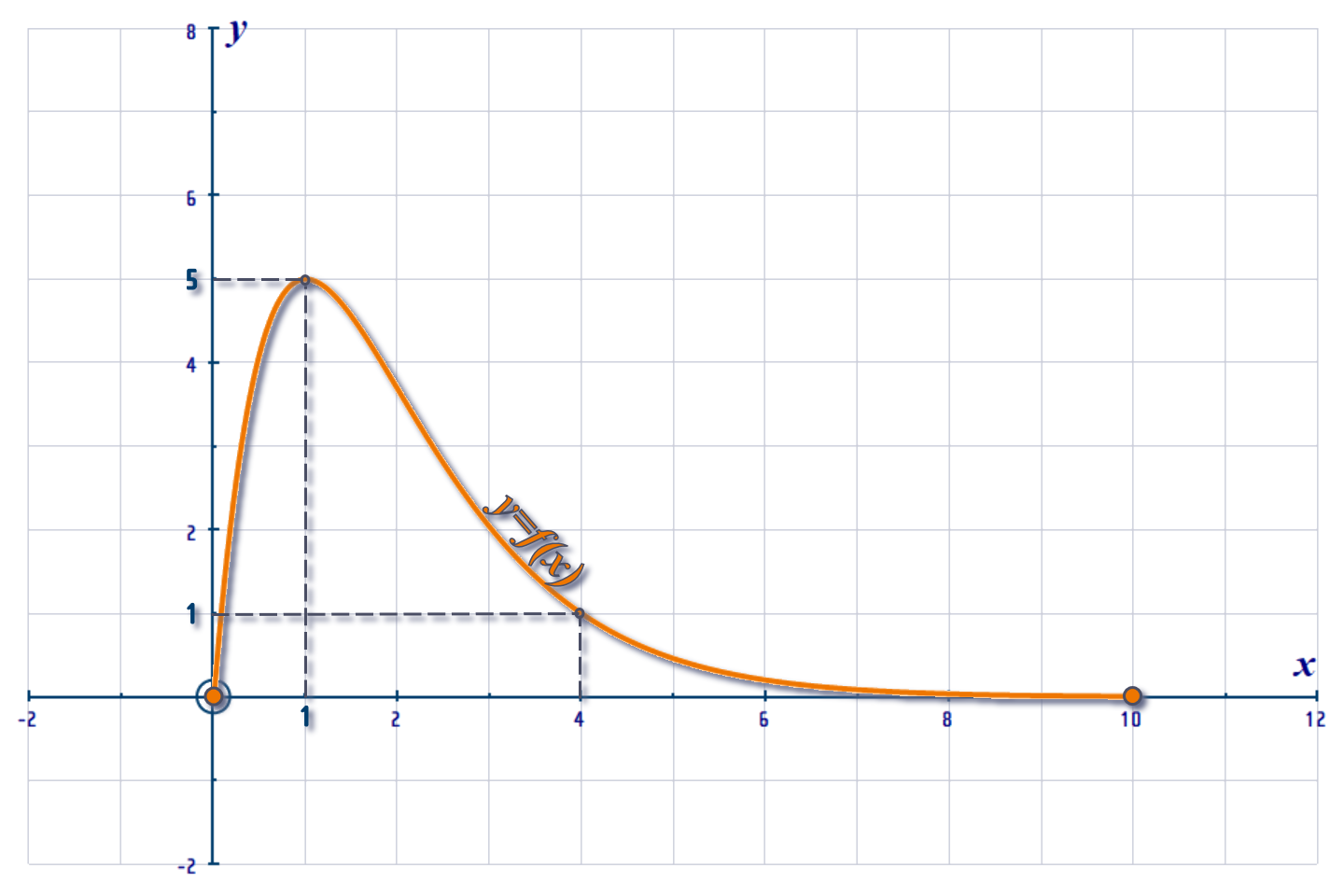
We are NOT told its equation: But we do know that \(f\left( x \right) \) is defined for \(0\leqslant x\leqslant 10\) and it has a root at \(x\,=\,0\) and another root at \(x\,=\,10\). The maximum point \(P\) is at \(\left( 1,5 \right) \).
It passes through the point \(Q\,=\,\left( 4, 1\right) \) and its gradient at \(Q\) is \(-\frac{3}{4}\)
The RANGE of \(y=f\left( x \right) \) is: \(0\leqslant yx\leqslant 5\)
Armed with this information about \(f\left( x \right) \) and the curve of \(y=f\left( x \right) \) (as shown above) and by using the same methods as in the movie, sketch the following curves.
Use squared or graph paper and use a different grid for each curve:
For each question, you must:
- State clearly the transformations you have made
- State the domain for which the transformed curve should be defined. Also state its range
- Identify the point \(P'\) (where \(P\,=\,\left( 1,5 \right) \) is on the transformed curve); and if \(P'\) is a maximum point
- Identify \(Q'\) (where \(Q\,=\,\left( 4,1 \right) \) is on the transformed curve); and state the gradient at \(Q'\)
- Identify where the points \(\left( 0,0 \right) \) and \(\left( 10,0 \right) \) have moved to; and determine if they are STILL roots
- Do you know the roots or the y-intercept of the transformed curve?
Question 9: Sketch: \(y=5\,-\,f\left( x+1 \right) \). You MUST state: (i) the domain, (ii) the range, (iii) \(P'\) (is it a still max?), (iv) \(Q'\) (and the gradient at \(Q'\)). PHEW!
Clue:
The FLOW-DIAGRAM is:
x ──────────► +1 ───────────► f(x) ──────────► ื-1 ──────────► +5
└─┬┘ └─┬─┘ └─┬┘
① ② ③
┌──────────┴──────────┐ │ │
+3 is before f(x): │ │
TRANSLATE -3 ALONG x ┌────────────┴─────┐ │
ื-1 is after f(x) │
REFLECT IN x-AXIS ┌────┴────┐
BLAH-BLAH
Don't forget: You got to locate the points P and Q AND you gotta give the gradient at Q
Question 10: Sketch: \(y=1\,-\,f\left( 4-x \right) \). You MUST state: (i) the domain, (ii) the range, (iii) \(P'\) (is it a still max?), (iv) \(Q'\) (and the gradient at \(Q'\)). PHEW!
Clue:
This is TRICKY. The problem we encountered in QUESTION 7 has RESURFACED!
In QUESTION 7, we used a workaround (we knew y = sin x is an ODD function, so we could re-write it)
But this time, we don't have that luxury!
So we need to find the SOLUTION to the "MULTIPLE TRANSFORMATIONS IN THE BRACKETS problem:
x ────────► ื-1 ─────────► +4 ─────────► f(x) ────────► ื-1 ────────► + 1
╘═════════╤════════╛
│
┌───────────────┴────────────────┐
┌──┘ You can see that there are TWO └──┐
│ transformations INSIDE the brackets! │
└──────────────────┬───────────────────┘
│
Well - the SOLUTION IS SIMP│E, you just REVERSE the order of those TWO:
│
┌─────────┴───────┐
x ────────► ื-1 ─────────► +4 ─────────► f(x) ─────────► ื-1 ────────► + 1
╘═╤═╛ ╘═╤═╛ ╘═╤═╛ ╘═╤═╛
│ ① │ │
│ │ │
② │ │
│ │
③ │
│
④
Here's an applet for you to check!
Complete this web lesson on separate paper from any other homework
The pass mark (to avoid additional homework on this topic) is: 8/10
Show full workings and highlight your answers
|
|




