Exercise 10.1Complex NumbersImaginary NumbersOne way of solving a quadratic is to use the quadratic formula: - b ± √ b² - 4ac 2a . Part of this equation (b² - 4ac), is called the Discriminant. In the past, we have used the Discriminant in this way: ┌───────────────┐
│ Discriminant: │
│ b² - 4ac │
└───┬───┬───┬───┘
┌─────────────────┘ │ └─────────────────┐
│ │ │
┌───────┴──────┐ ┌──────┴───────┐ ┌──────┴───────┐
│ b² - 4ac > 0 │ │ b² - 4ac = 0 │ │ b² - 4ac < 0 │
└───────┬──────┘ └──────┬───────┘ └──────┬───────┘
╔═══════╧══════╗ ╔═════════╧═════════╗ ╔═════╧═══════╗
║TWO real roots║ ║One (repeated) root║ ║No real roots║
╚══════════════╝ ╚═══════════════════╝ ╚═════════════╝
Strangely, even though we knew that negative numbers can't be square-rooted, we didn't simply say "NO ROOTS", we said, "NO REAL ROOTS", implying that there might be some "non-real" roots? If we allow ourselves to assign a value to: √-1: Let: √-1 = ⅈ (ⅈ stands for 1-unit of an imaginary number)
Then, actually, we allow ourselves to square-root all negative numbers: e.g. √-4 = √4×-1 = √4 × √-1 └┬┘ └─┬┘ └─┐┌──┘ = 2ⅈ e.g. √-2.25 = √2.25×-1 = √2.25 × √-1 └─┬──┘ └─┬┘ └──┐ ┌──┘ = 1.5ⅈ Imaginary numbers can be added to and subtracted from other imaginary numbers: e.g. 2ⅈ + 1.5ⅈ = 3.5ⅈ And, since we defined ‘ⅈ’ as √-1: √-1 = ⅈ
SQR SQR
-----------
-1 = ⅈ²
Which means that the product or quotient of two imaginary numbers will always be a real number: e.g. 2ⅈ × 1.5ⅈ = 3ⅈ² = 3(-1) = -3 Complex NumbersWhen a real number (such as ‘2’) is added to an imaginary number (such as ‘3ⅈ’), the answer cannot be simplified: e.g. 2 + 3ⅈ = 2+3ⅈ └┬┘ └─┬┘ └──┬─┘ real imaginary complex So, the answer is called a complex number... Complex numbers can be added/subtracted: ┌────────────┬───────────┐ e.g. (2 + 3ⅈ) + (2 - ⅈ) = 4 + 2ⅈ └─┬─┘ └─┬┘ └─┬┘ └────────────┴─────────────┘ And, they can be multiplied: ┌────────┬───┐
│ ▼ ▼
(2 + 3ⅈ)×(2 - ⅈ) = 4 - 2ⅈ + 6ⅈ - 3ⅈ²
│ ▲ ▲ └───┬───┘ └┬┘ ┌───────────┐
└────┴───┘ │ └────┤ Remember: │
│ ┌────┤ ⅈ² = -1 │
┌┴─┐ ┌┴─┐ └───────────┘
= 8 + 4ⅈ - 3(-1)
= 8 + 4ⅈ + 3
= 11 + 4ⅈ
ConjugatesThe conjugate of the complex number a + bⅈ is: a - bⅈ When a complex number is multiplied by its conjugate, the answer is always a real number: ┌────────┬───┐
│ ▼ ▼
(2 + 3ⅈ)×(2 - 3ⅈ) = 4 - 6ⅈ + 6ⅈ - 9ⅈ²
│ ▲ ▲ └───┬───┘ └┬┘ ┌───────────┐
└────┴───┘ cancel └────┤ Remember: │
┌───┤ ⅈ² = -1 │
┌┴─┐ └───────────┘
= 4 - 9(-1)
= 13
┌───────┬───┐
│ ▼ ▼
(2 + ⅈ)×(2 - ⅈ) = 4 - 2ⅈ + 2ⅈ - ⅈ²
│ ▲ ▲ └───┬───┘ └┬┘ ┌───────────┐
└───┴───┘ cancel └─────┤ Remember: │
┌─────┤ ⅈ² = -1 │
┌┴─┐ └───────────┘
= 4 - (-1)
= 5
This property helps us to divide complex numbers. In the same way as we "Rationalise the Denominator" of a surd, we "Realise the Denominator" of a complex fraction by multiplying both the top and the bottom by the conjugate of the denominator: (2 + 3ⅈ) ÷ (2 - ⅈ) = 2 + 3ⅈ 2 + ⅈ . = (2 + 3ⅈ)(2 - ⅈ) ◄─ Did this before ─────┐ (2 + ⅈ)(2 - ⅈ) ◄───── Did this before ─┼─────┐ │ │ = 11 + 4ⅈ ◄───────────────────────┘ │ 5 ◄─────────────────────────────┘ = 11 + 4ⅈ 5 5 Square-root of a Complex NumberAt this stage in our understanding of complex numbers, it is quite difficult to square-root a complex number and the method we will use only works for a few select examples... Later, we will learn a method that makes it much easier to square-root a complex number... For now, the method is: e.g. Find: √15 + 8ⅈStep 1: Since we don't know the answer, let's call it: a + bⅈ: √15 + 8ⅈ = a + bⅈ Step 2: Square both sides: 15 + 8ⅈ = (a + bⅈ)² 15 + 8ⅈ = a² + 2abⅈ + b²ⅈ² └┬┘ ┌───────────┐ └──────────┤ Remember: │ ┌────────┤ ⅈ² = -1 │ ┌┴─┐ └───────────┘ 15 + 8ⅈ = a² + 2abⅈ + b²(-1) 15 + 8ⅈ = (a²-b²) + 2abⅈ └─┬┘└──┬──┘ └──┬──┘└───┬──┘ ┌─┴────┴────────┴───────┴─────┐ ┌──────────────┐ Step 3: Equate the REAL parts To give Equate the imaginary parts two equations: └─┬────┬────────┬───────┬─────┘ └──────────────┘ ├────┼────────┘ │ │ └────────────────┤ ┌──┴─────┐ ┌───┴─┐ a²-b²=15 and 2ab=8 └──┬──┘ ┌───┴─────┐ │ b = 4/a │ └───┬─────┘ ┌───────────────────┘ a²-(4/a)²=15 a² - 16 = 15 a² ×a² ×a² ×a² ---------------- a4 - 16 = 15a2 a4 - 15a2 - 16 = 0 (a²+1)(a²-16) = 0 └─┬──┘└──┬──┘ no solns ┌──┴────────┐ a=4 or a=-4 └─┬─┘ └─┬──┘ b=1 b=-1 So: √15 + 8ⅈ = 4 + ⅈ or -4 - ⅈ └──┬──┘ Note: This is the required answer, since the question asked for +√15+8ⅈ Note: The square-root of a complex number is always another complex number. Question 1, part (a): We can write ⅈ7 as: ⅈ² × ⅈ² × ⅈ² × ⅈ
└┬┘ └┬┘ └┬┘ ┌───────────┐
└───┴───┴─────────────────┤ Remember: │
┌────┬────┬───────────────┤ ⅈ² = -1 │
┌┴─┐ ┌┴─┐ ┌┴─┐ └───────────┘
(-1)×(-1)×(-1)× ⅈ
Which simplifies to... Question 1, part (b): We can write ⅈ-3 as: ⅈ-2 × ⅈ-2 × ⅈ
1/ⅈ² × 1/ⅈ² × ⅈ
└┬┘ └┬┘ ┌───────────┐
└────┴──────────────────┤ Remember: │
┌────────┬────────────────┤ ⅈ² = -1 │
┌┴─┐ ┌┴─┐ └───────────┘
1/(-1) × 1/(-1) × ⅈ
Which simplifies to...
Question 2, part (a): When adding complex numbers: ┌───────────────────┐
add the real ‘bits’
└─────────┬─────────┘
┌────────────┬───────────┤
(3 + 5ⅈ) + (7 - ⅈ) = 11 + 4ⅈ
└─┬─┘ └─┬┘ └─┬┘
└────────────┴────────────┤
┌───────────┴────────────┐
add the imaginary ‘bits’
└────────────────────────┘
Question 3, part (a): When subtracting complex numbers: ┌────────────────────────┐
subtract the real ‘bits’
└───────────┬────────────┘
┌────────────┬───────────┤
(3 + 5ⅈ) ─ (7 - ⅈ) = -4 + 6ⅈ
└─┬─┘ └─┬┘ └─┬┘
└────────────┴────────────┤
┌─────────────┴───────────────┐
subtract the imaginary ‘bits’
└─────────────────────────────┘
Question 4, part (a): Multiply out just as normal: ┌────────┬───┐
│ ▼ ▼
(2 + ⅈ)×(3 - 4ⅈ) = 6 - 8ⅈ + 3ⅈ - 4ⅈ²
│ ▲ ▲ └───┬───┘ └┬┘ ┌───────────┐
└────┴───┘ │ └────┤ Remember: │
│ ┌────┤ ⅈ² = -1 │
┌┴─┐ ┌┴─┐ └───────────┘
= 6 - 5ⅈ - 4(-1)
= 6 - 5ⅈ + 4
= … - …ⅈ
Question 4, part (d): (3 + 4ⅈ) and (3 - 4ⅈ) are CONJUGATES If you call the first one z (i.e. z = 3 + 4ⅈ), then you can call the second one z* (i.e. z* = 3 - 4ⅈ) Whenever we multiply conjugates, the answer will be real: z·z* is always real!
Question 4, part (f): We can treat this as a BINOMIAL EXPANSION: \[{ \left( 1+i \right) }^{ 3 }=\\ \quad \quad \quad \quad \begin{matrix} 1 & +\;3\quad & +\;3\quad & +\;1\quad \\ 1{ i }^{ 0 } & +\;3{ i }^{ 1 } & +\;3{ i }^{ 2 } & +\;1{ i }^{ 3 } \end{matrix}\] Then simplify the \{{i}^{0}\), \{{i}^{1}\), \{{i}^{2}\)...
Question 5, part (a): A fraction is not simplified unless the denominator is REAL We need to to "Realise the Denominator" (multiply both the top and bottom of the fraction by (1 + ⅈ) - which is also called the conjugate of (1 - ⅈ): = 2 (1 + ⅈ) (1 - i)(1 + ⅈ) = … + …ⅈ 1 - ⅈ² └┬┘ ┌───────────┐ └────────────────┤ Remember: │ │ ⅈ² = -1 │ └───────────┘ = … + …ⅈ 2 = … + …ⅈ Question 5, part (b): Again, we need to to "Realise the Denominator" (multiply both the top and bottom of the fraction by = (3 + ⅈ) (4 + 3ⅈ) (4 - 3ⅈ)(4 + 3ⅈ) = 12 + 13ⅈ + 3ⅈ² 16 - 9ⅈ² └┬┘ ┌───────────┐ └────────────┤ Remember: │ │ ⅈ² = -1 │ └───────────┘ = … + …ⅈ 25 = … + …ⅈ or 1(… + …ⅈ) 25 25 25 └──────────────┬─────────────┘ either of these is OK as the answer
Question 5, part (g): The conjugate of ⅈ is just: ⅈ
Question 6, part (a): Expanding the R.H.S: ┌───────┬───┐
│ ▼ ▼
(3 + ⅈ)×(2 - 3ⅈ) = 6 - …ⅈ + …ⅈ - 3ⅈ²
│ ▲ ▲ └────┬────┘ └┬┘ ┌───────────┐
└───┴───┘ │ └─────────┤ Remember: │
│ ┌────────┤ ⅈ² = -1 │
┌┴─┐ ┌┴─┐ └───────────┘
= 6 - …ⅈ - 3(-1)
= 6 - …ⅈ + 3
= 9 - …ⅈ
And (in case you didn't already see the answer): x + yⅈ = 9 - …ⅈ └─┬┘└──┬──┘ └─┬─┘└───┬┘ Step 3: Equate the REAL parts └────┼────────┘ │ Equate the imaginary parts └───────────────┘ x=9 & y=… Question 6, part (b): You know that you need to simplify the fraction first (multiply top and bottom by 1+ⅈ), then equate the real parts and equate the imaginary parts...
Question 6, part (d): This is simple: equating the real parts and equate the imaginary parts: x + yⅈ = 2 + 0ⅈ └─┬┘└──┬──┘ └─┬─┘└───┬┘ Equate the REAL parts └────┼────────┘ │ Equate the imaginary parts └───────────────┘
Question 7, part (d): So the common denominator is: 2 + 3 = 3 + ⅈ 2 + ⅈ (3 + ⅈ)(2 + ⅈ) Which gives us: 2 + 3 = 13 + …ⅈ 3 + ⅈ 2 + ⅈ (3 + ⅈ)(2 + ⅈ) But, we can't leave our answer like that! Expanding the denominator: 2 + 3 = 13 + …ⅈ 3 + ⅈ 2 + ⅈ 5 + …ⅈ And finally, we need to "Realise the Denominator" (multiply both the top and bottom of the fraction by (5 - …ⅈ)
Question 7, part (f):
POLAR FORM:
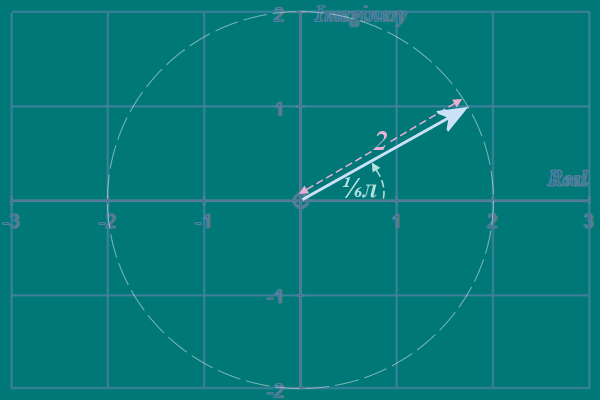
\(\color{#e8b0d3}{R}\left( \cos {\color{#9ad6d5}{\theta} } \;+\; i\sin { \color{#9ad6d5}{\theta} } \right)\) is the polar form of a complex number For instance: \(\color{#e8b0d3}{2}\left( \cos { \color{#9ad6d5}{⅙\pi} } \; +\; i\sin { \color{#9ad6d5}{⅙\pi} } \right)\) represents a complex number - the number is the point that is reached by a stick of length \(\color{#e8b0d3}{2}\), rotated at \(\color{#9ad6d5}{⅙\pi}\) from the x-axis:
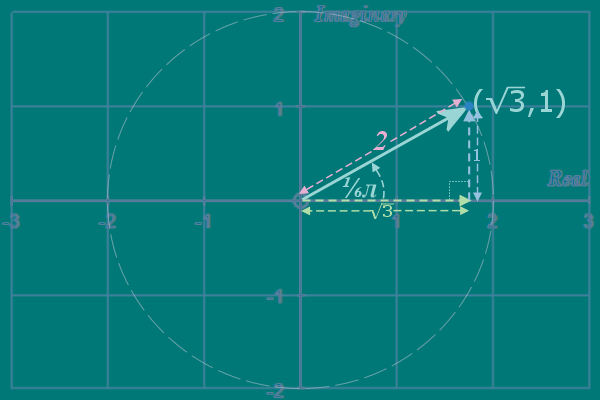
Using a bit of simple trigonometry, we can work out the x- and y- coordinates of the point at the end of this stick:
The x-coordinate is found by: \(\color{#e8b0d3}{2} \cos { \color{#9ad6d5}{⅙\pi }}\) Hence \(\color{#e8b0d3}{2}\left( \cos { \color{#9ad6d5}{⅙\pi} } \; +\; i\sin { \color{#9ad6d5}{⅙\pi} } \right)\) would give us both coordinates - and we will use this notation A LOT (we'll abbreviate it as: \(\color{#e8b0d3}{2}cⅈs\color{#9ad6d5}{{ ⅙\pi }}\)) We have TWO choices: We can work out: \(\cos { ⅓\pi }\) and \(\sin { ⅓\pi }\), then re-write as: \(\left(\color{#62be53}{ \frac { 1 }{ 2 } }\;+\; \color{#2b83c3}{\frac { ... }{ 2 }} i \right) ^{ 3 }\) Alternatively, we could just expand it leaving the \(\cos { ⅓\pi }\) and \(\sin { ⅓\pi }\) as they are and fill in the numerical values later - this second way is messy, but interesting...
Question 8, part (a): This is rather a clumsy method, but for now, it is the only method we have to find the square-root: Step 1: Since we don't know the answer, let's call it: a + bⅈ: √3 - 4ⅈ = a + bⅈ Step 2: Square both sides: 3 - 4ⅈ = (a + bⅈ)² 3 - 4ⅈ = a² + 2abⅈ + b²ⅈ² └┬┘ ┌───────────┐ └───────────┤ Remember: │ ┌──────────┤ ⅈ² = -1 │ ┌┴─┐ └───────────┘ 3 - 4ⅈ = a² + 2abⅈ + b²(-1) 3 - 4ⅈ = (a²-b²) + 2abⅈ └─┬┘└──┬──┘ └──┬──┘└───┬──┘ ┌─┴────┴────────┴───────┴─────┐ ┌──────────────┐ Step 3: Equate the REAL parts To give Equate the imaginary parts two equations: └─┬────┬────────┬───────┬─────┘ └──────────────┘ ├────┼────────┘ │ │ └────────────────┤ ┌──┴────┐ ┌──┴───┐ a²-b²=3 and 2ab=-4 └┐ └──┬───┘ └┐ ┌───┴──────┐ │ │ b = -2/a │ │ └───┬──────┘ ├──────────────────┘ a²-⎧-2⎫²= 3 ⎩ a⎭ a² - 4 = 3 a² ×a² ×a² ×a² ---------------- a4 - 4 = 3a2 a4 - 3a2 - … = 0 (a²+…)(a²-…) = 0 └─┬──┘└──┬──┘ no solns ┌──┴────────┐ a=… or a=… └─┬─┘ └─┬──┘ b=1 b=-1 So: √3 - 4ⅈ = … - ⅈ or -… + ⅈ If the question had said solve \({ z }^{ 2 }\;=\;3\;-\;4i\), then we'd give both answers, but it said find \(\sqrt{3\;-\;4i}\), we can just give the positive answer...
Question 8, part (b): Using the same method we used in part (a): Step 1: Since we don't know the answer, let's call it: a + bⅈ: √21 - 20ⅈ = a + bⅈ Step 2: Square both sides: 21 - 20ⅈ = (a + bⅈ)² 21 - 20ⅈ = a² + 2abⅈ + b²ⅈ² └┬┘ ┌───────────┐ └───────────┤ Remember: │ ┌──────────┤ ⅈ² = -1 │ ┌┴─┐ └───────────┘ 21 - 20ⅈ = a² + 2abⅈ + b²(-1) 21 - 20ⅈ = (a²-b²) + 2abⅈ └─┬┘└──┬──┘ └──┬──┘└───┬──┘ ┌─┴────┴────────┴───────┴─────┐ ┌──────────────┐ Step 3: Equate the REAL parts To give Equate the imaginary parts two equations: └─┬────┬────────┬───────┬─────┘ └──────────────┘ ├────┼────────┘ │ │ └────────────────┤ ┌──┴─────┐ ┌──┴────┐ a²-b²=21 and 2ab=-20 └┐ └──┬────┘ └┐ ┌───┴───────┐ │ │ b = -10/a │ │ └───┬───────┘ ├──────────────────┘ a²-⎧-10⎫² = 21 ⎩ a ⎭ a² - 100 = 21 a² ×a² ×a² ×a² ------------------ a4 - 100 = 21a2 a4 - 21a2 - … = 0 (a²+……)(a²-……) = 0 └─┬──┘└──┬──┘ no real ┌──┴────────┐ solns a=…… or a=…… └─┬─┘ └─┬──┘ b=…… b=…… So: √21 - 20ⅈ = … - …ⅈ or -… + …ⅈ
|