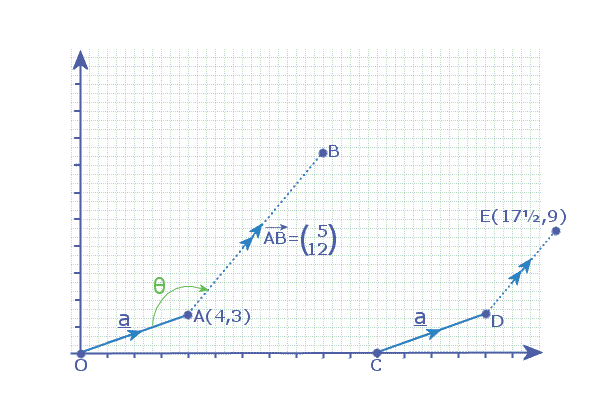
Exercise 9.2Vectors in 2-DImagine we have the points O, A, B, C, D & E as shown in the diagram below:
There are a few things we may want to find out about the diagram, such as:
All of these questions could happily be answered using our existing techniques; but we will instead learn to use 'Vector Techniques' to answer them. The reason being that these vector techniques can also be applied to 3-D problems, which we will encounter later...
Vector NotationYou are familiar with writing the coordinates of 'A' as (4,3)In vector notation, we may write the coordinates of 'A' as 4i
+ 3j
|
To find the relative vector PQ (from point 'P' to point 'Q')Simply subtract: Coordinates - Coordinates of 'Q' of 'P' |
e.g. Find the relative vector from AC:
AC = C - A ┌ ┐ ┌ ┐ ┌ ┐ AC = │11 │ - │ 4 │ = │ 7 │ (or: 7i - 3j) │ 0 │ │ 3 │ │-3 │ └ ┘ └ ┘ └ ┘
e.g. Find the relative vector OA:
OA = A - O ┌ ┐ ┌ ┐ ┌ ┐ OA = │ 4 │ - │ 0 │ = │ 4 │ (or: 4i + 3j) │ 3 │ │ 0 │ │ 3 │ └ ┘ └ ┘ └ ┘
So the relative vector OA is the same as the position vector
'A'
That is always true:
For any point 'P', the vector OP is the same as the position vector of 'P', which is essentially the same as the coordinates of 'P' |
e.g. 'E' has coordinates (17.5, 9). Find the vector OE:
┌ ┐ OE = │ 17.5 │ or OE = 17.5i + 9j │ 9 │ └ ┘
Again showing that there is little difference between the coordinates of a point, it's position vector and the relative vector from the origin to the point!
Adding Vectors
Relative Vectors can be added together to form a route to a
point
In the diagram, we are show that the vector which "takes us
from 'A' to 'B' is":
┌ ┐
AB = │ 5 │
│12 │
└ ┘
So, if we start from 'A' and then 'add' the vector which takes us from 'A to B'; then we end up at 'B':
OB = OA + AB ┌ ┐ ┌ ┐ ┌ ┐ OB = │ 4 │ + │ 5 │ = │ 9 │ (or: 9i + 15j) │ 3 │ │12 │ │15 │ └ ┘ └ ┘ └ ┘
So, the coordinates of 'B' are: (9, 15)
e.g. The point 'P' has coordinates (7, -2) and the vector PQ is -2i + 3j. Find the coordinates of Q:
OQ = OP + PQ ┌ ┐ ┌ ┐ ┌ ┐ OQ = │ 7 │ + │-2 │ = │ 5 │ (or: 5i + j) │-2 │ │ 3 │ │ 1 │ └ ┘ └ ┘ └ ┘
So, the coordinates of 'Q' are (5, 1)
The length of a Vector
If a vector is given by:┌ ┐ PQ = │ p │ or PQ = pi + qj │ q │ └ ┘ Then its length is given by: |PQ| = √ pイ + qイ |
e.g. Find the length of the vector OA in the diagram:
┌ ┐ OA = │ 3 │ |OA| = √ 3イ + 4イ │ 4 │ └ ┘ = 5 units
e.g. Find the length of the vector AB in the diagram:
┌ ┐ AB = │ 5 │ |OA| = √ 5イ + 12イ │12 │ └ ┘ = 13 units
e.g. Find the length of the vector OB in the diagram:
Earlier, we found the coordinates of 'B' were (9, 15) ┌ ┐ OB = │ 9 │ |OB| = √ 9イ + 15イ │15 │ └ ┘ = 17.49 units
Equivalent Vectors
In the diagram; the vector OA is labelled 'a' (it is common to name relative vectors using a small letter, underlined).
But you'll notice that the vector CD is also labelled 'a'. This means that the vector CD is both the same length and the same direction as the vector OA:
┌ ┐
CD = │ 4 │
│ 3 │
└ ┘
e.g. Since we now know CD, find the coordinates of 'D':
OD = OC + CD ┌ ┐ ┌ ┐ ┌ ┐ OD = │11 │ + │ 4 │ = │15 │ (or: 15i + 3j) │ 0 │ │ 3 │ │ 3 │ └ ┘ └ ┘ └ ┘
So, the coordinates of 'D' are: (15, 3)
e.g. Hence find the relative vector DE:
DE = E - D ┌ ┐ ┌ ┐ ┌ ┐ AC = │17ス│ - │15 │ = │2.5│ (or: 2.5i - 6j) │ 9 │ │ 3 │ │ 6 │ └ ┘ └ ┘ └ ┘
Parallel Vectors
Parallel vectors have the same direction, but different
lengths.
It is fairly easy to spot parallel vectors when they are written
in the column vector format; because there will be a 'constant'
that one vector can be multiplied to get the other:
AC AB ┌ ┐ ┌ ┐ │2.5│ 覧ラ2覧> │ 5 │ So: 2AC = AB │ 6 │ 覧ラ2覧> │12 │ └ ┘ └ ┘
Which tells us that they ARE parallel; but also that AB
is twice as long as AC
e.g. Are the vectors: PQ = 6i + 4j and RS = 3i + 2j parallel?
PQ RS ┌ ┐ ┌ ┐ │ 6 │ 覧ラス覧> │ 3 │ So: スPQ = RS │ 4 │ 覧ラス覧> │ 2 │ └ ┘ └ ┘
e.g. The points L, M, N and P have coordinates; (5,3), (8,5), (4,8) & (-2,4) respectively. Describe the shape LMNP:
Start with a quick sketch of the shape on a grid...
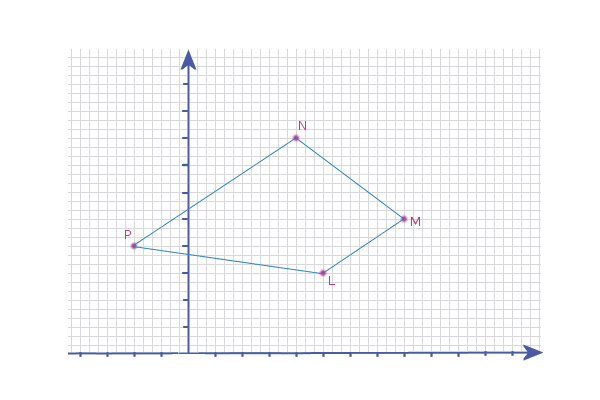
So, the sides of the shape are LM, MN, NP and PL
LM = M - L ┌ ┐ ┌ ┐ ┌ ┐ LM = │ 8 │ - │ 5 │ = │ 3 │ ═══════╗ │ 5 │ │ 3 │ │ 2 │ ═══════╣ └ ┘ └ ┘ └ ┘ ║ ║ MN = N - M ║ ┌ ┐ ┌ ┐ ┌ ┐ ║ MN = │ 4 │ - │ 8 │ = │-4 │ ║ │ 8 │ │ 5 │ │ 3 │ ║ラ-2 └ ┘ └ ┘ └ ┘ ║ ║ NP = P - N ║ ┌ ┐ ┌ ┐ ┌ ┐ ║ NP = │-2 │ - │ 4 │ = │-6 │ ◄══════╣ │ 4 │ │ 8 │ │-4 │ ◄══════╝ └ ┘ └ ┘ └ ┘ PL = L - P ┌ ┐ ┌ ┐ ┌ ┐ PL = │ 5 │ - │-2 │ = │ 7 │ │ 3 │ │ 4 │ │ 7 │ └ ┘ └ ┘ └ ┘ The first thing we notice is that the vectors: LM and NP are parallel No other vectors are parallel and a quadrilateral is only one pair of parallel sides is a: TRAPEZIUM
e.g. 'F' is a point along DE produced such that F is four times as far from D as E is. Find the coordinates of 'F':
Since we are told that 'F' is along the same line And is four times as far: DF = 4 ラ DE ┌ ┐ ┌ ┐ │...│ = 4 ラ │2.5│ │...│ │ 6 │ └ ┘ └ ┘ And so, by finding the vector OF, we can find the coordinates of 'F': OF = OD + DF ┌ ┐ ┌ ┐ ┌ ┐ OF = │15 │ + │10 │ = │25 │ (or: 25i + 27j) │ 3 │ │24 │ │27 │ └ ┘ └ ┘ └ ┘
e.g. 'R' is a point along AB such that it's distance from
'B' is three times it's distance from A.
Find the coordinates of 'R'.
Another way of saying this is to say: The vector AR is シ of the vector AB AR = シ ラ AB ┌ ┐ ┌ ┐ │...│ = シ ラ │ 5 │ │...│ │12 │ └ ┘ └ ┘ And so, by finding the vector OR, we can find the coordinates of 'R': OR = OA + AR ┌ ┐ ┌ ┐ ┌ ┐ OR = │ 4 │ + │5/4│ = │5.25│ (or: 5.25i + 6j) │ 3 │ │ 3 │ │ 6 │ └ ┘ └ ┘ └ ┘
The Vector Equation of a Line
In order to find the vector equation of a line, we need to know the position vector of any point on the line and the direction vector of the line (i.e. any relative vector that lies along the line or is parallel to the line):
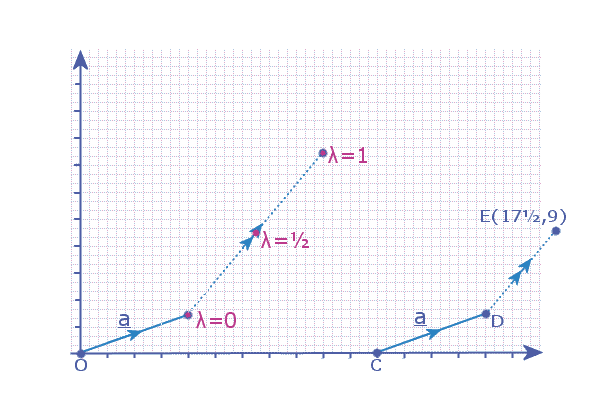
If 'P' and 'Q' are points on the line PQ, then the equation of the line PQ can be given by:r = OP + λ PQ Note: The vector equation of the same line can be written in numerous different ways that are not immediately obvious as being the same... |
We will deal with an example to show how easy this is to do,
before we go about explaining what it means...
e.g. Find the vector equation of the line AB in the diagram:
Since we know the vector position vector of 'A' and we know the relative vector 'AB' (which is a vector along the line)
r = OA + λ AB ┌ ┐ ┌ ┐ r = │ 4 │ + λ │ 5 │ or: r = (4i + 3j) + λ(5i + 12j) │ 3 │ │12 │ └ ┘ └ ┘ ╘═╦═╛ ╘═╦═╛ the position vector ╝ ╚ the dirn vector of a point on the line parallel to the line
So, this is the equation of the line "though 4i +3j" and "parallel to the vector 5i + 12j"
To understand this equation, we need to start by understanding what 'r' and 'λ' stand for:
-
'λ' is a scalar (that means "an ordinary number, not a vector"). It is the variable in the equation; so putting in different values of 'λ' generates the different 'points' on the line...
-
'r' is the position vector of any point on the line AB
For example: If we put in λ=0 into the equation:
┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + 0 │ 5 │ = │ 4 │ (or: 4i + 3j) │ 3 │ │12 │ │ 3 │ └ ┘ └ ┘ └ ┘ Which is the position vector of the point 'A' on the line AB
If we put in λ=1 into the equation:
┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + 1 │ 5 │ = │ 9 │ (or: 9i + 15j) │ 3 │ │12 │ │15 │ └ ┘ └ ┘ └ ┘ Which is the position vector of the point 'B' on the line AB
If we put in λ=ス into the equation:
┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + ス │ 5 │ = │6.5│ (or: 6.5i + 9j) │ 3 │ │12 │ │ 9 │ └ ┘ └ ┘ └ ┘ Which is the position vector of 'M', the midpoint of AB
If we put in λ=シ into the equation:
┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + シ │ 5 │ = │5.25│ (or: 5.25i + 6j) │ 3 │ │12 │ │ 6 │ └ ┘ └ ┘ └ ┘ Which is the position vector of the point 'R' on the line AB
So, because we used the point 'A' and vector 'AB' to form
the equation of the line; when we put in 'λ=0' we get the
point 'A' and when be put in 'λ=1' we get the point 'B' and
when we put in 'λ=1/2' we get the point which is halfway
between 'A' and 'B'
[Kinda reminds you of the Grand Old Duke
of York - when they were up they were up, when they were down
they were down and when they were halfway up...]
Actually; we could have found the equation of the line AB in a different way:
We could have started with the point 'B' and the vector AB:
r = OB + η AB ┌ ┐ ┌ ┐ r = │ 9 │ + η │ 5 │ (or: r = (9i + 15j) + η(5i + 12j) │15 │ │12 │ └ ┘ └ ┘ Note: Since I have written the equation a different way, I have used a different variable 'η' so we don't get mixed up...
Although this is still the equation of the line AB; this time when we put in 'η=0' we get the point 'B'; when we put in 'η=-1' we get the point 'A' and when we put in 'η=1' we get the point with coordinates (14, 27); which is further along the line AB...
Alternatively; we could have used the two points A(4, 3) and R(5.25, 6) to find the line AB:
We know the vector position vectors of 'A' & 'R' So we can find the relative vector 'AR': AR = R - A ┌ ┐ ┌ ┐ ┌ ┐ AR = │5シ │ - │ 4 │ = │1シ │ │ 6 │ │ 3 │ │ 3 │ └ ┘ └ ┘ └ ┘ Now we can find the equation of the line AR (which is really the same line as AB): r = OA + κ AR ┌ ┐ ┌ ┐ r = │ 4 │ + κ │1シ │ │ 3 │ │ 3 │ └ ┘ └ ┘
So, the question is posed; how can we tell that these three
equations all represent the same line?
We'll answer that in a
little while
e.g. Find the equation of the line CD:
Since we know the vector position vector of 'C' And we know the relative vector 'CD' (is the same as OA)
r = OC + μ CD ┌ ┐ ┌ ┐ r = │11 │ + μ │ 4 │ or: r = (11i + 0j) + μ(4i + 3j) │ 0 │ │ 3 │ └ ┘ └ ┘ ╘═╦═╛ ╘═╦═╛ the position vector ╝ ╚ the dirn vector of a point on the line parallel to the line
e.g. Find the equation of the line through 9i + 2j, parallel to 5i + 2j:
We know the vector position vector of a point on the line '9i + 2j' And we know a vector parallel to the line '5i + 2j;
r = OA + λ AB ┌ ┐ ┌ ┐ r = │ 9 │ + λ │ 5 │ or: r = (9i + 2j) + λ(5i + 2j) │ 2 │ │ 2 │ └ ┘ └ ┘ ╘═╦═╛ ╘═╦═╛ the position vector ╝ ╚ the dirn vector of a point on the line parallel to the line
Finding a Particular Point on a Line
1. You may be asked to find a point for a particular value of 'λ':
e.g. Find the point on r = (4i + 3j) + λ(5i + 12j) where λ=4:
┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + 4 │ 5 │ = │24 │ = 24i + 51j │ 3 │ │12 │ │51 │ └ ┘ └ ┘ └ ┘
2. You may be asked to find a point given a particular 'x' or 'y' coordinate:
e.g. Find the point on r = (4i + 3j) + λ(5i + 12j) where x=-1:
Since we don't know the 'y' coordinate of the point where x=-1 we can call the point (-1, ?): ┌ ┐ ┌ ┐ ┌ ┐ │ 4 │ + λ │ 5 │ = │-1 │ 覧覧► 4 + 5λ = -1 覧覧► λ = -1 ═╗ │ 3 │ │12 │ │ ? │ 覧覧► 3 + 12λ = ? ◄══════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = -1 Substituting into the BOTTOM ROW gives: y = -9 So the point is (-1, -9)
e.g. Find the point on r = (2i - 8j) + λ(3i + 5j) where y=2:
Since we don't know the 'x' coordinate of the point where y=2 we can call the point (?, 2): ┌ ┐ ┌ ┐ ┌ ┐ │ 2 │ + λ │ 3 │ = │ ? │ 覧覧► 3 + 3λ = ? ◄════════════╗ │-8 │ │ 5 │ │ 2 │ 覧覧► -8 + 5λ = 2 覧覧► λ = 0 ═╝ └ ┘ └ ┘ └ ┘ Solving the BOTTOM gives: λ = 2 Substituting into the BOTTOM ROW gives: x = 9 So the point is (9, 2)
e.g. Does the point (7, 11) lie on r = (3i + 3j) + λ(2i + 5j):
Pretend we don't know the 'y' coordinate of the point where x=7 we can call the point (7, ?): ┌ ┐ ┌ ┐ ┌ ┐ │ 3 │ + λ │ 2 │ = │ 7 │ 覧覧► 3 + 2λ = 7 覧覧► λ = 2 ═╗ │ 3 │ │ 5 │ │ ? │ 覧覧► 3 + 5λ = ? ◄═════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = 2 Substituting into the BOTTOM ROW gives: x = 13 So the point where x is '7' is (7, 13), NOT (7, 11) So (7, 11) is not on the line!!
Finding where a line intercepts the axes
1. To find where a line intercepts the x axis; we put 'y=0'
e.g. Find where r = (3i + 4j) + λ(2i - 8j) intercepts the x axis:
We put y=0, so we can call the point (?, 0): ┌ ┐ ┌ ┐ ┌ ┐ │ 3 │ + λ │ 2 │ = │ ? │ 覧覧► 3 + 3λ = ? ◄════════════╗ │ 4 │ │-8 │ │ 0 │ 覧覧► 4 - 8λ = 0 覧覧► λ = ス ═╝ └ ┘ └ ┘ └ ┘ Solving the BOTTOM ROW gives: λ = 1/2 Substituting into the TOP ROW gives: x = 4 So the point is (4, 0)
2. To find where a line intercepts the y axis; we put 'x=0'
e.g. Find where r = (i + 5j) + λ(2i - 6j) intercepts the y axis:
We put x=0, so we can call the point (0, ?): ┌ ┐ ┌ ┐ ┌ ┐ │ 1 │ + λ │ 2 │ = │ 0 │ 覧覧► 1 + 2λ = 0 覧覧► λ = -ス ═╗ │ 5 │ │-6 │ │ ? │ 覧覧► 5 - 6λ = ? ◄══════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = -1/2 Substituting into the BOTTOM ROW gives: y = 8 So the point is (0, 8)
Identifying Equivalent Equations
Before, we learnt that there are many different ways of writing the vector equation of the line AB
We posed the question;
"How do we tell that: r =
(9i + 15j) + λ(5i
+ 12j) and r = (4i +
3j) + κ(1シi
+ 3j)
represent the same line?"
1. The direction vectors must be parallel:
d.v. of eqn 2 d.v. of eqn 1 ┌ ┐ ┌ ┐ │1シ │ 覧ラ4覧> │ 5 │ │ 3 │ 覧ラ4覧> │12 │ └ ┘ └ ┘
2. We must prove that the 'point' given on the 2nd equation is also a point that lies on the 1st equation:
┌ ┐ So, we know that │ 4 │ lies on the second line │ 3 │ └ ┘ We have to check it this point also lies on the first line: Ignore the 'y' coordinate and call the point (4, ?) ┌ ┐ ┌ ┐ ┌ ┐ │ 9 │ + λ │ 5 │ = │ 4 │ 覧覧► 9 + 5λ = 4 覧覧► λ = -1 ═╗ │15 │ │12 │ │ ? │ 覧覧► 15 + 12λ = ? ◄══════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = -1 Substituting into the BOTTOM ROW gives: y = 3 So the point where x is 4 is: (4, 3)
Which shows that both lines pass through the point (4, 3) and since we have already shown that the direction vectors are parallel, we can say that these two equations represent the SAME line...
Finding where two Lines Intersect
To find where two lines intersect:
-
Make them equation to each other
-
Read the "Top Line" of this vector equation and call this equation (1)
-
Read the "Bottom Line" of this vector equation and call this equation (2)
-
Solve simultaneously to find 'λ' and 'オ'
-
Put the value of 'λ' back into it's equation to find the point of intersection
e.g. Find where the lines AB [ r = (4i + 3j) + λ(5i + 12j) ] and CD [ r = (11i) + オ(4i + 3j) ] intersect:
┌ ┐ ┌ ┐ ┌ ┐ ┌ ┐ │ 4 │ + λ │ 5 │ = │11 │ + μ │ 4 │ 覧・#9658; 4+ 5λ = 11+4μ 覧・#9658; 4+5λ = 11+ 5μ │ 3 │ │12 │ │ 0 │ │ 3 │ 覧・#9658; 3+12λ = 3μ 覧・#9658; 1+4λ = μ └ ┘ └ ┘ └ ┘ └ ┘ Multiply bottom eqn by 5 and subtract・/font> Solving equations simultaneously gives: λ=-1 and μ=-3 Putting λ = -1 into line (1): ┌ ┐ ┌ ┐ ┌ ┐ r = │ 4 │ + -1 │ 5 │ = │-1 │ = -i - 9j │ 3 │ │12 │ │-9 │ └ ┘ └ ┘ └ ┘
So, they meet at (-1, -9)
Converting a Vector Equation to Cartesian Form
The method is as follows:
-
Replace 'r' with (x, y)
-
Read the "Top Line" of this vector equation and call this equation (1)
-
Read the "Bottom Line" of this vector equation and call this equation (2)
-
Make 'λ' the subject of BOTH equations and then make them equal to each other. This is the Cartesian equation
e.g. Find the Cartesian Equation for: r = (4i
+ 3j) + λ(5i
+ 12j):
┌ ┐ ┌ ┐ r = │ 4 │ + λ │ 5 │ │ │ 3 │ │12 │ ▼ └ ┘ └ ┘ ┌ ┐ ┌ ┐ ┌ ┐ │ x │= │ 4 │ + λ │ 5 │ <= x = 4 + 5λ │ y │ │ 3 │ │12 │ <= y = 3 + 12λ └ ┘ └ ┘ └ ┘ So: λ = x - 4 and: λ = y - 3 5 12 => x - 4 = y - 3 5 12
You may wish to tidy this up by making 'y' the subject (but it's really not necessary...)
In practice, it is not necessary to go through this, because you can 'see' how to get quickly from one form to the other
e.g. Find the Cartesian Equation for: r = (5i + 2j) + λ(7i + 3j):
=> x - 5 = y - 2 7 3
e.g. Find the Cartesian Equation for: r = (2i -3j) + λ(4i + 5j):
=> x - 2 = y + 3 4 5
e.g. Find the Cartesian Equation for: r = (2i + 1j) + λ(5i -1j):
=> x - 2 = y - 1 5 -1
e.g. Find the Cartesian Equation for: r = (2j) + λ(-i + 3j):
=> x - 0 = y - 2 -1 3
e.g. Find the Cartesian Equation for: r = (5i + 2j) + λ(7i):
=> x - 5 = y - 2 7 0 But this one doesn't seem to make sense, because we can't "divide by 0" In fact, the only way it comes close to making sense is if y=2 (then the top of the fraction would also be zero) => In fact the equation is: y = 2
Question 1, part (a): The coordinates of 'B' are found by first finding the position vector OB:
OB = OA + AB ┌ ┐ ┌ ┐ ┌ ┐ OB = │ 4 │ + │ 3 │ = │.. │ (or: ..i + ..j) │ 1 │ │ 9 │ │.. │ └ ┘ └ ┘ └ ┘
So, the coordinates of 'B' are: (.., ..)
Question 1, part (b): So we are told that AP = 1/3 AB. Since we know AB, we can work out AP:
AB AP ┌ ┐ ┌ ┐ │ 3 │ 覧ラ⅓覧> │.. │ │ 9 │ 覧ラ⅓覧> │.. │ └ ┘ └ ┘
Then, by first finding the position vector OP, we can find
the coordinates of 'P'...
Question 1, part (c): A direction vector along the line AB is '3i + 9j':
┌ ┐ i.e. │ 3 │ │ 9 │ └ ┘
[since it the vector AB which IS along the line]
But:
┌ ┐ │ 1 │ │ 3 │ └ ┘
Is also a direction vector along the line [any multiple of 'i + 3j' is a direction vector of the line].
We always try to use the simplest (or most cancelled down) direction vector, which is 'i + 3j'
So, to complete the equation of the line, we need to know any point on the line. In facto, we already know 3 points on the line, so we can use either one of these.
So the equation of the line could be written:
┌ ┐ ┌ ┐
r = │ 4 │ + λ │ 1 │ or: r = (4i + j) + λ(i + 3j)
│ 1 │ │ 3 │
└ ┘ └ ┘
╘═╦═╛ ╘═╦═╛
the position vector ╝ ╚ the dirn vector
of a point on the line parallel to the line
But it could equally well be written as:
┌ ┐ ┌ ┐
r = │ 7 │ + λ │ 1 │ or: r = (7i + 10j) + λ(i + 3j)
│10 │ │ 3 │
└ ┘ └ ┘
Or as:
┌ ┐ ┌ ┐ r = │ 5 │ + λ │ 1 │ or: r = (5i + 4j) + λ(i + 3j) │ 4 │ │ 3 │ └ ┘ └ ┘
Question 1, part (d): To see if 0i - 11j lies on the line:
Pretend we don't know the y-coordinate of the point where x=0 we can call the point (0, ?):
┌ ┐ ┌ ┐ ┌ ┐ │ 4 │ + λ │ 1 │ = │ 0 │ 覧覧► 4 + λ = 0 覧覧► λ = -4 ═╗ │ 1 │ │ 3 │ │ ? │ 覧覧► 1 + 3λ = ? ◄══════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = -4 Substituting into the BOTTOM ROW gives: y = .. So the point where x is '0' is (0, ・ Therefore (0, -11) [is/is not]? on the line!!
Question 2: The coordinates of 'A' and the position vector 'OA' are (more or less) the same thing:
┌ ┐
OA = │ 4 │ (or: 4i + 3j)
│ 3 │
└ ┘
And the same applies for OB...
Now we are told that OP = 2/3 OA, which means we can find OP:
OA OP ┌ ┐ ┌ ┐ │ 4 │ 隣2/3・gt; │8/3│ │ 3 │ 隣2/3・gt; │.. │ └ ┘ └ ┘
Question 3, part (a): So, we are told:
┌ ┐ a = │12 │ │ 0 │ └ ┘
and we are told b = ...
We can find the vector AB:
AB = B - A ┌ ┐ ┌ ┐ ┌ ┐ AB = │ 2 │ - │12 │ = │.. │ │10 │ │ 0 │ │.. │ └ ┘ └ ┘ └ ┘
And, since AX = 1/5 AB, we can find AX:
AB AX ┌ ┐ ┌ ┐ │.. │ 隣1/5・gt; │.. │ │.. │ 隣1/5・gt; │.. │ └ ┘ └ ┘
Finally, we can find OX since we know the vector from 'O' to 'A' and we know the vector from 'A' to 'X', we can add them to find the vector from 'O' to 'X':
OX = OA + AX ┌ ┐ ┌ ┐ ┌ ┐ OX = │12 │+ │.. │= │.. │ │ 0 │ │.. │ │.. │ └ ┘ └ ┘ └ ┘
So, we know the coordinates of 'X'
Question 3, part (b): From before, we know:
┌ ┐ b = │ 2 │ │10 │ └ ┘
And since we are told AY = nb:
b AY
┌ ┐ ┌ ┐
│ 2 │ 覧ラn覧> │2n │
│10 │ 覧ラn覧> │10n│
└ ┘ └ ┘
But we want to find BY (the vector from 'B' to 'Y')
So, we use the vector from 'B' to 'A' and then the vector from
'A' to 'Y':
BY = BA + AY ┌ ┐ ┌ ┐ ┌ ┐ BY = │.. │ + │2n │ = │2n+10 │ │.. │ │10n│ │10n-10 │ └ ┘ └ ┘ └ ┘
[You may not realise it and it is not relevant to
understanding the question, but this is really the vector
equation of a line]
Question 3, part (c): Now, we are told that the vector OX is parallel to the vector BY. That means there must be a number that one can be multiplied by to get the other [since we don't know the number, we can call it 'k']:
OX AY ┌ ┐ ┌ ┐ │10 │ 覧ラk覧> │2n+10 │ │ 2 │ 覧ラk覧> │10n-10 │ └ ┘ └ ┘
Which gives us two equations: 10k = 2n + 10 and 2k = ...
Which can be solved to find 'n'
Which means we now know AY
Which means we can find OY
Which means we can find the coordinates of 'Y'
Question 4, part (a): Since we know two points on the line, we can find a vector along the line:
AB = B - A ┌ ┐ ┌ ┐ ┌ ┐ AB = │-1 │- │-2 │= │.. │ │ 5 │ │ 3 │ │.. │ └ ┘ └ ┘ └ ┘
So, we can use one of the points on the line, together with this vector to get the equation of the line. So, if we use 'A' as our point on the line, the equation of the line would be:
┌ ┐ ┌ ┐ r = │-2 │ + λ │.. │ │ 3 │ │.. │ └ ┘ └ ┘
But, if we use 'B' as our 'point on the line' our answer would be:
┌ ┐ ┌ ┐ r = │-1 │ + λ │.. │ │ 5 │ │.. │ └ ┘ └ ┘
Note: These two lines are actually equivalent...
Question 4, part (b): If we remove the y coordinate from the
point (5, 15) and call it (5, y)
And then make the equation equal this, it tells us that λ =
...
And that y = ...
Which is NOT what it should be...
Question 4, part (c): Again, if we call the point (3, y)...
Question 5, part (a): So the line is:
┌ ┐ ┌ ┐ r = │ 0 │ + λ │ 1 │ │ 1 │ │ 2 │ └ ┘ └ ┘ Putting in λ = 2: A ┌ ┐ ┌ ┐ ┌ ┐ r = │ 0 │ + 2 │ 1 │ = │ 2 │ So A = 2i + 5j │ 1 │ │ 2 │ │ 5 │ └ ┘ └ ┘ └ ┘ Putting in λ = 5 ...
Question 6: To find where an equation meets the x axis, we make y=0 and so we make the equation equal (?, 0):
┌ ┐ ┌ ┐ ┌ ┐ │ 0 │ + λ │.. │ = │ ? │ 覧覧► 0 + λ = ? ◄════════════╗ │ 4 │ │.. │ │ 0 │ 覧覧► 4 - 2λ = 0 覧覧► λ = ・═╝ └ ┘ └ ┘ └ ┘ Solving the BOTTOM ROW gives: λ = ・ Substituting into the TOP ROW gives: x = ・ So the point is (・ 0)
To find where a line meets the y axis, we put x=0 and so we make the equation equal (0, y)...
Question 12: We need to find the direction vector of the line joining A to B and use this as the direction vector for our line (since they are parallel)...
Question 13: If we find the vector AB and we then find the vector BC, we'll see that they are parallel. And since both vectors pass through the same point ('B'), they must both lie along the same line (i.e. colinear).
Again, there are quite a few ways of writing the equation of the line, since we know three different points on the line. In any case, the direction vector of the line should be "-2i + 5j" since both directions cancel down to this.
Question 14: Line 1 passes through (2i + 5j) and has
direction vector (6i + 8j)
Line 2 passes through (2i + 5j) and has direction vector (3i +
4j).
These direction vectors are the same (since they are
parallel)
And both lines pass through the same point (2i + 5j)
So they are equivalent...
Question 15: It is easy to see that both lines have the same
direction vectors, so all we need to do is show that the point
(6i - 2j) does lie on line 1:
To do this, we call the point (6, ?) and make line 1 equal to this:
┌ ┐ ┌ ┐ ┌ ┐ │ 0 │ + λ │ 2 │ = │ 6 │ 覧覧► 0 + 2λ = 6 覧覧► λ = ・═╗ │-5 │ │ 1 │ │ ? │ 覧覧► -5 + λ = ? ◄════════════╝ └ ┘ └ ┘ └ ┘ Solving the TOP ROW gives: λ = ・ Substituting into the BOTTOM ROW gives: y = ・ Which shows that (6, 2) [is/is not]? on the line
Question 18, part (a): Start by writing each side of the equation in the familiar form i.e. (x-A)/B:
=> x - 0 = y - 3 4 2
So the equation must be:
┌ ┐ ┌ ┐ r = │ 0 │ + λ │ 4 │ or: r = (3j) + λ(4i + 2j) │ 3 │ │ 2 │ └ ┘ └ ┘
Note: Actually, it is better if the direction vector is
cancelled down to (2i + j)...
Question 18, part (c): Start by writing each side of the equation in the familiar form i.e. (x-A)/B:
=> x - -3 = y - 2 1 4
So the equation is...
Question 18, part (d): We want to write it in the usual form
i.e. (x-A)/B; but the only way we can do that in this case is:
(y-3)/0
As for the left hand side, well that can be anything:
Start by writing each side of the equation in the familiar form i.e. (x-A)/B:
=> x - A = y - 3 B 0
Where 'A' and 'B' can be ANY NUMBERS (except 'B' can't be zero). So, for instance, the equation could be:
┌ ┐ ┌ ┐
r = │ 1 │ + λ │ 1 │ or: r = ...
│ 3 │ │ 0 │
└ ┘ └ ┘
[I chose to replace 'A' and 'B' with '1' in this case...]