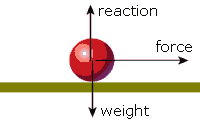
Web Lesson 4: MomentsSo far, we have only considered forces that act on a particle. These forces can only push or pull the particle:
But, if we have an object such as a long plank of wood, and we pivot it at one point, then we can apply forces to 'turn' the object.
This object cannot be modelled as a particle and the forces do not accelerate the particle in the way that we have covered previously. Instead, the force causes the plank to "turn":
'Turning forces' are called 'Moments'. Moments are measured in a new unit called "Newton-Metres" (Nm):
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
F = 20 N θ = 30° d = 2 |
Resolving our force, using the rod as the x-axis:
 |
Component of force that is perpendicular to the rod: 20 sin 30° = 10 N |
Now that we have resolved the force, we can find the moment:
In the diagram: Perpendicular force = 10 N ╗ d = 2 m ╠══ Moment = F × d Moment = ??? ╝ = 10 × 2 = 20 Nm
To produce the greatest moment, the force should be applied at 90° to the rod
In every-day use, we use levers because they provide a greater moment. For example, imagine using a short spanner to unscrew a nut:
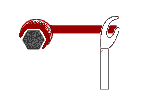
Now imagine using a longer spanner for the same job:

You know instinctively, that the longer spanner will make it easier. Now, knowing about moments can make that simple to understand. Imagine the maximum force your hand can exert is 200N and the spanner is only 10 cm long:
 |
F = 200 N ╗ d = 0.1 m ╠══ Moment = F × d Moment = ??? ╝ = 200 × 0.1 = 20 Nm |
But, using the longer (50 cm) spanner, our same 200N force produces a larger moment:
 |
F = 200 N d = 0.5 m Moment = 200 × 0.5 = 100 Mn |
e.g. 3: A door of width 2 m is hinged at one end and has a handle at the other end.
(a) Find the moment produced if I push the door using a force of 20 N at right angles to the door.
(b) What would the moment be if my force of 20 N makes an angle of 60° with the door?
(a): The hinge is where the door pivots, so we draw a pivot there (mark it like this: "Δ")
The 'push' is represented by an arrow as we always do with a force...
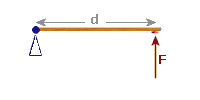 |
F = 20 N ╗ d = 2 m ╠══ Moment = F × d Moment = ??? ╝ = 20 × 2 = 40 Nm |
(b): Re-drawing our diagram with the force at 60° to the door:
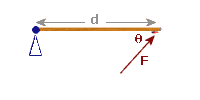 |
Component of force that is perpendicular to the rod: 20 sin 60° = 17.3 N |
Now that we have resolved the force, we can find the moment:
In the diagram: Perpendicular force = 17.3 N ╗ d = 2 m ╠══ Moment = F × d Moment = ??? ╝ = 17.3 × 2 = 34.6 Nm
e.g. 4: A car door has width 1.2 m and is hinged at one end
On the outside, there is a handle at the opposite end to the hinge. On the inside, there is a handle in the middle of the door
The door is stuck and so two people are trying to prise it open. Carlos is pulling the handle from outside using a force of 80 N. Jose is pushing the handle from inside using a force of 100 N
Find the total moment produced by the gruesome twosome
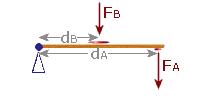 |
There are two moments in this diagram: |
||||
Moment due to Jose:
FB = 100 N (Carlos)
dB = 0.6 m
MomentB = F × d
= 100 × 0.6
= 60 Nm
|
Moment due to Carlos:
FA = 60 N (Jose)
dA = 1.2 m
MomentA = F × d
= 60 × 1.2
= 96 Nm
|
||||
Total Moment = 60 + 96 = 156 Nm |
|||||
Question 2: A spanner has length 200 cm. If I push down on the spanner with a force of 250 N, what will the moment produced be?
Clue: You diagram should look like this:
 |
F = ...
d = 2 m
Moment = ... × 2
= … Mn
|
Question 3: A 4 m wide ship door is stuck. Jack and Jill are both pushing the door, Jack using a force of 800 N in the middle of the door and Jill using a force of 500 N at the end opposite the hinge. Find the total moment produced
Clue: You diagram should look like this:
 |
There are two moments in this diagram: |
||||
Moment due to Jack:
FB = 800 N (Jack)
dB = … m
MomentB = F × d
= 800 × …
= ... Nm
|
Moment due to Jill:
FA = 500 N (Jill)
dA = … m
MomentA = F × d
= 500 × …
= ... Nm
|
||||
Total Moment = ... + ... = … Nm |
|||||
Equilibrium
In "Forces and Motion" we had to consider the forces acting on a particle. We needed to define which direction was positive and which was negative.
If the positive forces equal the negative forces, then we would say the particle was in equilibrium.
Since moments are "Turning Forces", we can't define "positive" and "negative", so instead we define which moments are "clockwise" and which are "anticlockwise":

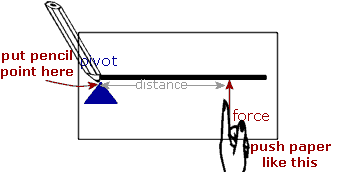
To decide if a moment is clockwise or anticlockwise, put your pencil point on the pivot and pull the paper in the direction of the force.
If the paper turns "clockwise", then the moment is a "Clockwise Moment":
So, in this case the moment is "Anti-clockwise".
For moments, equilibrium occurs if the clockwise moments equal the anticlockwise moments
Moments: Equilibrium
|
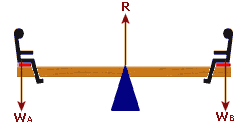
Take the example of a see-saw:

If a boy ("Henry") sits, on one side of the see-saw, then the see-saw will be unbalanced:

His weight will produce a "Clockwise Moment" (because his weight makes the plank turn in a clockwise direction):

Since there is no "Anti-clockwise Moment" to balance this, the see-saw will turn until it hits the ground:

If, instead "Henry" and his identical twin "Amritlal" both get on the see-saw:

Then there are two moments. Henry's weight still produces a "Clockwise Moment", but Amritlal's weight produces an "Anti-clockwise Moment" (because he is on the other side of the pivot):
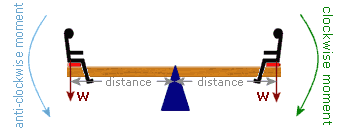
And, since they are both the same weight and are sitting the same distance from the pivot, the anti-clockwise moment equals the clockwise moment and the see-saw will remain balanced.
In practice, one of the twins will "kick-off" from the ground (providing an extra force which unbalances the moments) and that person will start to rise. Then the other twin will "kick-off" from the ground....
e.g. 5: A see-saw of total length 4 m is pivoted at its centre. Jane (mass 40kg) sits at one end. How far from the pivot should Joe (mass 50 kg) sit if the see-saw is to balance (use g = 10)?
We will use the abbreviations CWM for "Clockwise Moments" and ACWM for "Anti-clockwise Moments"
Anti-clockwise Moment:
WA = 400 N (Jane)
dA = 2 m
MomentA = 400×2
= 800
|
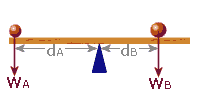 |
Clockwise Moment:
WB = ... N (Joe)
dB = 'x'
MomentB = 500×x
= 500x
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
800 = 500x
=> 1.6 = x
|
So Joe should sit 1.6 m from the pivot
e.g. 6: A see-saw of total length 4 m is pivoted at its centre
Jane (mass 40 kg) is sat on one end and Joe (mass 50 kg) is sat on the other
On which side and how far from the pivot should their child (Jamie, mass 25 kg) sit in order to balance the see-saw (use g = 10)?
Since Jane is lighter than Joe, it is obvious that Jamie will have to sit on the same side as Jane...
There are three forces to consider: The weight of Jane, called "WA" The weight of Jamie, called "WC" The weight of Joe, called "WB"
So, in our diagram, there are TWO anticlockwise moments:
Anti-clockwise Moments:
WA = 400 N (Jane)
dA = 2 m
MomentA = 400×2
= 800
Wc = 200 (Jamie)
dc = 'x'
Momentc = 200×x
= 250x
|
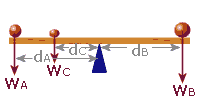 |
Clockwise Moment:
WB = 500 N (Joe)
dB = …
MomentB = 500×…
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
800 + 250x = ....
=> x = …
|
Jamie should sit 0.8 m from the pivot
Question 4: A see-saw of total length 8 m is pivoted at its centre. Sunil (mass 60 kg) sits at one end. Where should Priti (mass 80 kg) sit to balance it? (Use g = 10)
Clue: Your diagram should look like this:
Anti-clockwise Moment:
WA = 600 N (Sunil)
dA = 4 m
MomentA = 600×4
= 2400
|
 |
Clockwise Moment:
WB = … N (Priti)
dB = 'x'
MomentB = …×x
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
2400 = ...
=> … = x
|
So Priti should sit ... m from the pivot
Question 5: A see-saw of total length 6 m is pivoted at its centre. Gary sits at one end, and Betty (whose mass is half of Gary's) sits at the other. Where should Nisha (whose mass is 2/3 of Gary's) sit to balance it? (Use g = 10)
Clue: Since Betty is lighter, Nisha will have to sit on the same side of the see-saw as her:
There are three forces to consider: The weight of Betty, called "WA" The weight of Nisha, called "WC" The weight of Gary, called "WB"
Since we don't know Gary's weight, we can call it "W" - then Betty's weight is "½W" and Nisha's weight is "2/3 W":
Anti-clockwise Moments:
WA = ½W (Betty)
dA = 3 m
MomentA = ½W×3
= 1.5W
Wc = ⅔W (Nisha)
dc = x
Momentc = ⅔W×x
= ⅔Wx
|
 |
Clockwise Moment:
WB = W (Gary)
dB = …
MomentB = W×…
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
1.5W + ⅔Wx = ....
÷W ÷W ÷W
-------------------
1.5 + ⅔x = ...
=> x = …
|
Nisha should sit ... m from the pivot
Weight of the Plank
Up 'till now, we've ignored the weight of the plank in working out the moments. But, if the pivot is not placed in the centre of the plank, then we must also include the weight of the plank. This force is drawn onto our diagram as a vertical line placed halfway along the plank:
Now, as the questions become a little more detailed, it is VITAL to start with a clear diagram:
-
Decide where your pivot is and mark it with a "Δ"
-
Put in vertical arrows to show each weight (including the weight of the plank which acts from its centre)
-
Only label the distance of each weight from the PIVOT
e.g. 7: A plank of mass 20 kg and of length 10 m is pivoted 3 m from one end. A mass of 50 kg be placed along the shorter side in order to balance the system. How far from the pivot should it be placed (use g = 10)?
There are two forces to consider: The force exerted by the 50 kg mass, called "WA" The force exerted by the plank, called "WP" Start with a clear diagram and label the distance of each weight from the pivot: (The weight of the plank acts from its centre, which is 5 m from the end, but 2 m from the pivot)
Anti-clockwise Moment:
WA = 500 N (50 kg mass)
dA = 'x'
MomentA = 500×x
= 500x
|
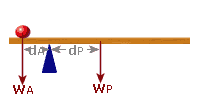 |
Clockwise Moment:
WP = … N (20 kg plank)
dP = 2
MomentP = …×2
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
500x = ...
=> x = …
|
So the mass needs to be placed 0.8 m from the pivot
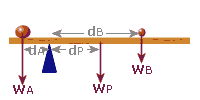
e.g. 8: A plank 'PQ' of mass 6 kg and of length 14 m is pivoted 5 m from end 'P'. A mass of 3 kg is placed at 'P'. How far from the pivot should a mass of 500 g be placed in order to balance the system (use g = 10)?
There are three forces to consider: The weight of the 3 kg mass, called "WA" The weight of the plank, called "WP" The weight of the 0.5 kg mass, called "WB" Start with a clear diagram and label the distance of each weight from the pivot: (The weight of the plank acts from its centre, which is 7 m from the end, but 2 m from the pivot)
Anti-clockwise Moment:
WA = 30 N (3 kg mass)
dA = 5 m
MomentA = 30×5
= 150
|
 |
Clockwise Moments:
WP = 60 N (Plank)
dP = 2
MomentP = 60×2
= 120
WB = … N (0.5 kg mass)
dB = 'x'
MomentB = …×…
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
150 = 120 + ....
=> … = x
|
So the 500g mass should be placed 6 m from the pivot
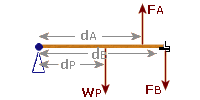
e.g. 9: A trap door of width 2.4 m and mass 80 kg sits horizontally on a kitchen floor and is hinged at one end. The other end of the door is bolted from the inside
Carlos is pulling on the handle, which is 2 m from the hinge with a force of 1500 N
Given that the bolt is starting to give, find the force exerted by the bolt
There are three forces to consider: The force exerted by Carlos, called "FA" The weight of the trap door, called "WP" The force of the bolt, called "FB" Start with a clear diagram and label the distance of each weight from the pivot: (The weight of the door acts from its centre, which is 1.2 m from from the pivot)
Anti-clockwise Moment:
FA = 1500 N (Carlos)
dA = 2 m
MomentA = 1500×2
= 3000
|
 |
Clockwise Moments:
WP = 800 N (800 kg door)
dP = …
MomentP = 800×…
= ....
FB = 'x' (bolt force)
dB = 2.4
MomentB = x×2.4
= 2.4x
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
3000 = .... + 2.4x
=> … = x
|
So the bolt exerts a force of 850 N
Question 6: A plank PQ of length 18 m and mass 12 kg is pivoted 6 m from end 'P'. What mass should be placed 1 m from end 'P' to balance it? (Use g = 10)
Clues: There are two forces to consider: The force exerted by the mass, called "WA" The force exerted by the plank, called "WP" Start with a clear diagram and label the distance of each weight from the pivot: (The weight of the plank acts from its centre, which is 9 m from 'P', but 3 m from the pivot) (The unknown mass is placed 1 m from end 'P', which is 5 m from the pivot)
Anti-clockwise Moment:
WA = W (unknown mass)
dA = 5
MomentA = W×5
= 5W
|
 |
Clockwise Moment:
WP = … N (12 kg plank)
dP = 3
MomentP = …×3
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
5W = ...
=> W = …
|
"W" stands for the weight, so the mass is found be dividing that by ...
Question 7: A plank of length 7 m and mass 2 kg is pivoted 3 m from end 'A'. A mass of 4 kg is added 1 m from end 'B'
What mass should be added at end 'A' to balance it? (Use g = 10)
Clues: Sorry - no clues for this question
Upthrust (Reaction at Pivot)
The pivot does not produce a "moment" itself, but it does produce a reaction force (which is at 90° to the plank):
Imagine in the example above that Henry's weight is 600 N and Amritlal's weight is also 600 N. Then the total downward force is 1200 N
This must be balanced be a reaction force at the pivot:
Upthrusts
|
So, the reaction force at the pivot will equal the upthrusts:
So, in the case of our see-saw, the reaction must be 1200 N
e.g. 10: A rod PQ of mass 12 kg and of length 4 m has a mass of 24 kg is placed ½ m from end 'P'
(a) Where should the pivot be placed in order to balance the system?
(b) What is the reaction at the pivot?
Use g = 10
Let the distance of the pivot from end 'P' = 'x'
So, distance from the pivot to the centre of mass of the rod is '2-x'
And, the distance from the pivot to the 24 kg mass is 'x-½'
Anti-clockwise Moment:
WA = 240 N
dA = 'x-½'
MomentA = 500×(x-½)
= 500(x-½)
|
 |
Clockwise Moment:
WP = … N
dP = 2-x
MomentP = …×(2-x)
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
500(x-½) = ...
=> x = …
|
So the pivot needs to be 1 m from end 'P'
Now, adding in the reaction force to our diagram:
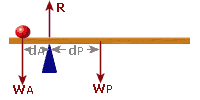 |
forces UP = forces DOWN R = 240 + 120 R = 360 N |
Question 8: A rod 'AB' of length 12 m and mass 8 kg has a 2 kg mass attached 1 m from end 'A'
(a) Where should it be pivoted in order to balance?
(b) What is the reaction force at the pivot
(Use g = 10)
Clues: The pivot obviously needs to be "BETWEEN" the 80 N weight and the 20 N weight...
Let the distance from the pivot to end 'A' be 'x'
So, the distance of the 20 N weight for the pivot is 'x-…'
And, the distance of the weight of the plank from the pivot is '6-…'
Two Pivots
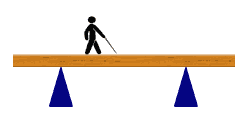
It is often the case that a plank will be rested on two pivots (to create a makeshift bridge to walk across):

In such cases, we have two possible pivots:
And since each pivot also produces a reaction force, these are all of our forces:
We can take moments about either of the pivots
When we take moments about Pivot A, we ignore the reaction force at Pivot A but we must put in the reaction force at Pivot B. So, when we are taking moments about Pivot A, our diagram looks like this:
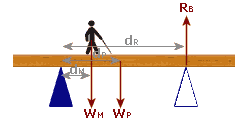
And, when we are taking moments about pivot B, our diagram looks like this:
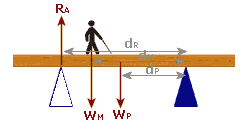
And remember we can also use:
total reaction forces = total downwards forces:
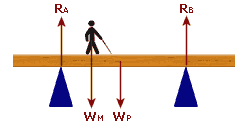
e.g. 11: A plank 'PQ' of length 8 m and mass 20 kg is rested on two supports, 'A' and 'B'; one 1 m from end 'P' and the other 2 m from end 'Q'. I have mass 80 kg and I stand in the middle of the plank. Find the two reaction forces (use g = 10)
So, let's start with a diagram showing all of the forces, including the reaction at each pivot...
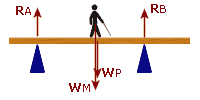 |
The diagram shows all the forces acting on the plank |
But, in order to take Moments about 'A' we must ignore the reaction force at 'A' and think of 'A' as the only pivot:
There are three forces to consider: The reaction at 'B', called "RB" My weight, called "WM" The weight of the plank, called "WP"
Anti-clockwise Moment:
RB = 'x'
dB = 5 m
MomentB = x×5
= 5x
|
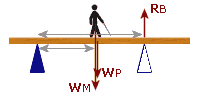 |
Clockwise Moments:
WM = 800 N (my weight)
dM = 3 m
MomentM = 800×3
= 2400
WP = 200 N (plank)
dP = 3 m
MomentP = 200×3
= 600
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
5x = 2400 + 600
=> x = …
|
So the reaction at 'B' is 600 N
In order to find the reaction at 'A', we could take moments about 'B'
Or, alternatively, we can remember that the total UPwards forces must equal the total DOWNwards forces:
 |
Forces UP = Forces DOWN RA + 600 = 800 + 200 RA = 400 N |
e.g.12: A plank 'PQ' of length 5 m and mass 20 kg is rested on two supports, 'A' and 'B'; one 1 m from end 'P' and the other 1 m from end 'Q'. I have mass 80 kg and am standing above the 2nd pivot
(a) Find the two reaction forces
I now start walking towards end 'B'
(b) How far from the pivot will I be when the plank starts to topple?
So, let's start with a diagram showing all of the forces, including the reaction at each pivot...
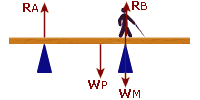 |
The diagram shows all the forces acting on the plank |
But, in order to take Moments about 'A' we must ignore the reaction force at 'A' and think of 'A' as the only pivot:
There are three forces to consider: The reaction at 'B', called "RB" The weight of the plank, called "WP" My weight, called "WM" Since 'A' is the pivot, label in the distances of WP, WM and RB from 'A'
Anti-clockwise Moment:
RB = 'x' (Reaction at B)
dB = 3 m
MomentA = x×3
= 3x
|
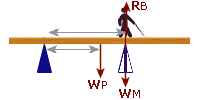 |
Clockwise Moments:
WP = 200 N (Plank)
dP = 1.5 m
MomentP = 200×1.5
= ...
WM = 800 N (My weight)
dM = 3 m
MomentM = 800×3
= ....
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
3x = .... + ...
=> x = …
|
So the reaction at 'B' is 900 N
In order to find the reaction at 'A', we could take moments about 'B'
Or, alternatively, we can remember that the total UPwards forces must equal the total DOWNwards forces:
 |
Forces UP = Forces DOWN RA + 900 = 800 + 200 RA = 100 N |
Now, the final part of this question is interesting...
Did you notice that the reaction at 'B' is much greater than the reaction at 'A'. As I walk further along the plank (towards end 'B'), the reaction at 'A' will get less and less...
At some point, the reaction at 'A' will become ZERO. If I carry on walking after this, then the plank will topple:
Anti-clockwise Moment:
WP = 200 N (Plank)
dP = 1 m
MomentA = 200×1
= 200
|
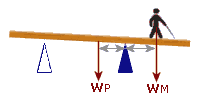 |
Clockwise Moment:
WM = … N (My weight)
dM = x
MomentM = …×x
= ...
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
200 = ...
=> … = x
|
So the plank will start to topple when I am ¼ m from the pivot at 'B'
Question 9: A plank PQ of length 3 m and mass 30 kg is supported by two pivots, one 0.5 m from end P and the other 1 m from Q
(a) Find the reactions at the pivots
A mass of 10 kg is added 1 m from end 'P'
(b): Find the reactions now
(use g = 10)
Clues: For part (a), let's start by naming the pivot near end 'P' as 'A', and the other pivot can be 'B'
We can use 'A' as the actual pivot and put in a reaction force at 'B'
So, our diagram will have these forces:
The reaction at 'B', called "RB" The weight of the plank, which is "300 N"
All we need to do now is make sure we have the correct distances of each force from the pivot (i.e. … m and 1.5 m) and use:
ANTI-CLOCKWISE MOMENTS = CLOCKWISE MOMENTS
We can find RA buy including it in the diagram again, and then using: Forces UP = forces DOWN
For part (b), out diagram looks like this (since 'A' is the pivot, RA has been erased):
Anti-clockwise Moment:
RB = 'x' (Reaction at B)
dB = 1.5 m
MomentA = x×1.5
= 1.5x
|
 |
Clockwise Moments:
WP = … N (Plank)
dP = 1 m
MomentP = …×1
= ...
WM = 100 N (10 kg mass)
dM = … m
MomentM = 100×…
= ....
|
╚══════════════════════╗ ╔══════════════════════╝
▼ ▼
Anti-clockwise moments = Clockwise Moments
1.5x = .... + ...
=> x = …
|
Again, putting RA back in and using: Forces UP = Forces DOWN to find RA...
Question 10: A plank of length 6 m and mass 25 kg is supported by two pivots, one at end 'A' and the other 2 m from end 'B'
(a) Find the reactions
(b) What mass must be placed at end 'B' in order to make it topple?
(Use g = 10)
Clues: Sorry - you have to do this all on your lonesome...