Exercise 3CDynamicsNewton's second law of motion states, "when the forces on a particle are unbalanced
(i.e. the
resultant force is NOT zero), it will accelerate or
decelerate"
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dynamics The direction in which the particle is accelerating is defined as 'positive'.We then use:(forces in +ve dirn) — (forces in -ve dirn) = ma |
e.g. A car of mass 600 kg is accelerating along a horizontal road. At a particular moment, the frictional force is 200 N and the engine force is 1400 N. Find its acceleration at that moment. (Use g = 10)
200N |
|
1400N |
(+ve forces) - (-ve forces) = m a
1400 - 200 = 600a
=> a = 2 m/s²
|
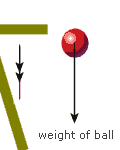
e.g. A ball of mass 100g is falling through the air. Assuming the frictional force is constant at 0.18 N, find it's acceleration. Why is the assumption unrealistic? (Use g = 9.8)
Mass = 100g = 0.1kg => weight = 0.1 × 9.8 = 0.98 N |
||
|
|
0.08N 0.98N |
(+ve forces) - (-ve forces) = m a 0.98 - 0.18 = 0.1a => a = 8 m/s² |
e.g. A car of mass 800 kg is travelling along a smooth road at 20 m/s. The driver applies a braking force of 400 N. What is the deceleration. After how long will the car come to rest and what distance will is travel during the deceleration?
Strangely, although I know the car will be decelerating (so the accln will be to the left), I have still drawn the accln to the right... The reason is that I want my answer to be negative After all, it is a deceleration |
|||
400N |
|
(+ve forces) - (-ve forces) = m a
0 - 400 = 800a
=> a = -½ m/s²
|
|
u = 20 v = u + at v = 0 0 = 20 + (-½)t a = -½ t = 40 sec t = ??? s = ??? s = ½ t (u + v) = ½(40)[20 + 0] = 400 m
e.g. A car of mass 700 kg is travelling along a rough road at 20 m/s where the friction force is a constant 50N. The driver applies a braking force of 300 N. Find the deceleration
300N 50N |
|
(+ve forces) - (-ve forces) = m a
0 - 350 = 700a
=> a = -½ m/s²
|
e.g. A car of mass 500 kg with an engine force of 800N and accelerates at 5 m/s² along a rough surface. Assuming that the friction force is constant, find the size of the friction force
F |
|
300N |
(+ve forces) - (-ve forces) = m a
300 - F = 500a
=> a = 2 m/s²
|
e.g. A ball accelerates at 6 m/s² when dropped. Assuming a constant air resistance of 4 N. Find it's mass in grams. (Use g = 10)
Let the mass = m kg So, weight = 10m N |
||
|
|
4 N 10m |
(+ve forces) - (-ve forces) = m a
10m - 4 = m (6)
=> 16m = 4
=> m = ¼ kg = 250g
|
e.g. For fun, a man decides to take his weighing scales into the lift with him. He stands on the scales and they record a weight of 800 N. He then presses the button to take him to the top floor. The lift accelerates at 2 m/s² and the reading on the weighing scales changes. By finding the new resultant force on the scales, find the new reading. (Use g = 10)
We need to consider the two forces acting on the man: 1) Is his weight (which we know is 800N acting downwards) 2) Is the (upward) force of scales on which he is standing |
||
|
|
F 800N |
(+ve forces) - (-ve forces) = m a
F - 800 = 80 (2)
=> F = 960 N
=> So, the scales are pushing him upwards
with a force of 960 N
So the reading on the scales is 960 N
|
Link with the equations for Constant Acceleration
Earlier (Ex 2D & 2E), we used the equations for constant acceleration:
|
|
The link between these two techniques is the acceleration...
So, if we are given the force,
we use the technique of dynamics to find the acceleration...
... then we use the equations of motion to find whatever else is
required
Or, if we are asked to find the force (and we aren't told the acceleration), we use the equations of motion to find the acceleration, then the technique of dynamics to find the force...
Question 1: Since we are given the force, we use the technique of dynamics to find the acceleration...
(+ve forces) - (-ve forces) = ma (4000) - (0) = (1000)a => a = ...
...and then we use the equations for uniform acceleration:
Now, since we know: u = 0 v = 10 a = ... Using: v² = u² + 2as s = ??? (10)² = (0)² + 2(...)s => s = ...
Question 2: This time, we are asked to find the force, so we start by using the equations of motion to find the acceleration...
u = 0 t = 6 s = 50 Using: s = ut + ½at² a = ??? (50) = (0)(6) + ½a(6)² => a = ...
...and then we use the technique of dynamics to find the force:
(+ve forces) - (-ve forces) = ma
(P) - (0) = (54)(...)
=> P = ... Newtons
Question 3: We need to start by finding the acceleration, using:
(+ve forces) - (-ve forces) = ma
(900) - (0) = (0.005)(a)
=> a = ...
And now we can find the velocity that it leaves the barrel using:
u = 0 a = ... s = 0.6 v = ???
etc...
Question 4: Using the equations of motion to find the acceleration...
Then using: (+ve forces) - (-ve forces)
= ma
to find the force...
Question 5: u = 20, v = 0, t = 8, a = ???
Etc...
Question 6: Remember: 1 Tonne = 1000 kg:
u = 5 v = 0 s = 0.8 a = ??? Etc...
Then use: (+ve forces) - (-ve forces) = ma
to find the acceleration
Question 7: Starting with the case when there are only 2 horses: The carriage moves at steady speed, which we treat exactly the same as "stationary". There are three forces on the carriage, one force from each horse as well as the friction force:
left forces = right forces F = 1200 + 1200
So, the friction is 2400N
Now, when there are 4 horses, the carriage will accelerate:
(+ve forces) - (-ve forces) = ma
(4800) - (2400) = (1000)a
=> a = ...
Question 8: So, when the bullet is travelling in the wood, there is only one force (the resistance of the wood):
(+ve forces) - (-ve forces) = ma
(0) - (8000) = (0.05)a
=> a = ... [As expected, it is negative indicating a deceleration...]
Now using the equations of motion...
u = 800 v = 0 a = ... s = ???
Question 11: So the diagram is like this:
So, its weight is: 5 × 9.8 = 49 N |
|||
a |
|
20 49 |
(+ve forces) - (-ve forces) = ma
(49) - (20) = 5a
=> a = ...
|
So: u = 0 a = ... s = 100 t = ??? |
|||
Question 12: It is travelling upwards, so air resistance is acting downwards:
So, it's weight is: 2 × 9.8 = 19.6 N In this question, I have defined upwards as +ve, because that is the direction I prefer to think of as +ve |
|||
│ ▲ ▲ │ 19.6 |
|
5 |
(+ve forces) - (-ve forces) = ma
(0) - (19.6 + 5) = 2a
=> a = ...
[We knew it would be -ve]
|
So: u = 30 a = ... v = 0 s = ??? t = ??? |
|||
Question 13: We are using the vector version of the equation:
(+ve forces) - (-ve forces) = ma
It is still the same, except the forces and the acceleration are written as vectors:
We are told that, when t=0, the only force is: ┌ ┐ │ 1 │ │ 1 │ │-1 │ └ ┘ Using (+ve forces) - (-ve forces) = ma ┌ ┐ ┌ ┐ ┌ ┐ │ 1 │ │ 0 │ │ ? │ │ 1 │ - │ 0 │ = 5 │ ? │ │-1 │ │ 0 │ │ ? │ └ ┘ └ ┘ └ ┘ Which tells us the acceleration is: ┌ ┐ │ 0.2 │ │ 0.2 │ │-0.2 │ └ ┘ Then, using the vector form of: v = u + at ┌ ┐ ┌ ┐ ┌ ┐ │ ? │ │ 7 │ │ 0.2 │ │ ? │ = │ 2 │ + 20 │ 0.2 │ │ ? │ │ 5 │ │-0.2 │ └ ┘ └ ┘ └ ┘ Which tells us the final velocity is: ┌ ┐ │ ... │ │ ... │ │ ... │ └ ┘