|
Web Lesson #36 Angles in Polygons
WL#36 Regular and Irregular Polygons
The Interactive Web-Lesson below has questions embedded
So do it carefully, as your answers are sent to me!
- When a question pops up, if you want to see the movie again, click 🅷🅸🅳🅴 (in the top right corner)
- You CAN'T retry a flopped question: So PAY ATTENTION and THINK!
- Anytime you click on the © 2022 Math'scool you'll skip back to the previous section...
1. Naming Polygons
The number of sides is generally assigned the letter \(n\)
\(n=3\): A \(3\)-sided polygon is called a triangle
A regular triangle is called an equilateral-triangle; it looks like this:
 \(n=4\): A \(4\)-sided polygon is called a quadrilateral
A regular quadrilateral, termed a square, looks like this:
 \(n=5\): A \(5\)-sided polygon is called a pentagon
No name is assigned to the regular-pentagon (other than to say regular):
\(n=6\): A \(6\)-sided polygon is called a hexagon
A regular hexagon looks like this:
 \(n=7\): A \(7\)-sided polygon is called a heptagon
A regular heptagon looks like this:
 \(n=8\): An \(8\)-sided polygon is called a octagon
A regular octagon looks like this:
 \(n=9\): A \(9\)-sided polygon is called a nonagon
A regular nonagon looks like this:
 \(n=10\): A \(10\)-sided polygon is called a decagon
A regular decagon looks like this:
 \(n=11\): An \(11\)-sided polygon is called a hendecagon
A regular hendecagon looks like this:
 \(n=12\): A \(12\)-sided polygon is called a dodecagon
A regular dodecagon looks like this:
 \(n=20\): A \(20\)-sided polygon is called a icosagon
A regular icosagon looks like this:
 As \(n\) increases, the polygon approaches the shape of a circle!
As \(n\rightarrow \infty \)

2. Regular and Irregular Polygons
Regular Polygons
For a regular polygon, all their angles are the same as each other and all of the lengths are the same as each other
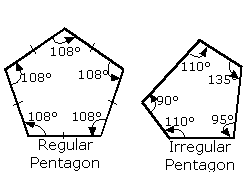
Some of the rules below apply to ALL polygons (regular or irregular).
Other rules only apply to regular polygons
2. All Polygons (Regular & Irregular):
Rule 1:
Sum of Exterior Angles = \(360°\)
(regardless of how many sides it has...)
Rule 2:
Sum of Interior Angles = \(180(n-2)\)
(where n = number of sides)
For a triangle (i.e. n = 3):
Sum of the interior angles = 180(3-2) = 180° (we knew that already!)
For a quadrilateral (i.e. n = 4):
Sum of the interior angles = 180(4-2) = 360° (we knew that already!)
For a pentagon (i.e. n = 5):
Sum of the interior angles = 180(5-2) = 540° (we probably didn't know that already!)
Example 1: Find the missing angle in this polygon
We've got a choice here...
...we could use RULE 1 (Sum of Exterior Angles = 360), or RULE 2 (Sum of Interior Angles = \(180\left( n-2 \right) \)
I'll do both, so you can see which you prefer...
Using RULE 1:
So, first of all, we have to find all of the other exterior angles
The exterior angle corresponding to the 110° interior-angle (at the top) is: 180°-110° = 70°
The exterior angle corresponding to the interior-angle \(x\) (at the bottom) is: \(180-x\)
And, since the sum of the exterior angles must equal 360°:
70° + 100° + (180-x)° + 90° + 60° = 360°
└─────────────────────────┬──────┘
┌──┴─────┐
500° - x = 360°
-360 + x -360° + x
----------------------
=> 140° = x
Using RULE 2:
So, first of all, we have to find all of the other interior angles
The angle on the left (100°) is an exterior angle. The interior angle corresponding to this is \(180°-100°=\color{#2b83c3}{80°}\)
Similarly, the interior angle on the right is \(\color{#2b83c3}{120°}\)
Now, since the number of sides: \(\color{#e54239}{n=5}\):
Sum of Interior Angles = \(180\left(\color{#e54239}{5}-2 \right)=\color{#2b83c3}{540°}\)
So, adding up all the Interior Angles and making it total 540°
80° + 110° + 120° + 90° + x° = 540°
└───────────────────────┬────┘
┌────┴────┐
400° + x° = 540°
-400° -400°
------------------
x° = 140°
Question 1:
Click here to print off this polygon
Having first worked out the value of \(x\), fill in the numerical value of each angle onto the drawing
Then, dust off your protactor, and measure each angle and see if (to the nearest 1°) the angles correspond to your calculations
(They should; because I drew this one - to scale...)
Hints
They've marked on the EXTERIOR-ANGLES of this polygon, so we should use RULE 2:
Rule 2:
Sum of Exterior Angles = 360°
(regardless of how many sides)
Now, most of the angles
they've shown are turning clockwise
but some angles turn anti-clockwise
└───────┬───────┘
│
│
│
└────────────
┌────────►
│
│
│
─────────────────────┤
├────────────────►
│
│
│
└──────────►
In fact, that doesn't matter, so you can just carry on with RULE 2
But just in case it does bother you, I've
rotated those three, so that all of the angles
turn clockwise So, applying RULE 2, simply means these angles have to add up to 360°
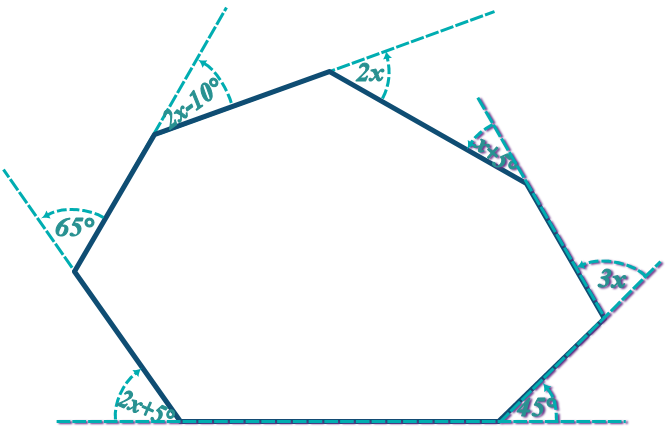
(2x) + (x+5°) + (3x) + (45°) + (2x+5°) + (65°) + (2x+10°) = 360°
└────────────────────────────┬───────────────────────────┘
........... = 360°
Now, input this value of x into each individual angle:
2x = ...
x+5° = ...
3x = ...
2x+5° = ...
2x+10° = ...
Finally, print off the polygon and measure the angles with your rusty (?) protractor,
checking they match up, innit!
Question 2:
Find the missing interior angle in this hexagon:
Hints
For this question, we should switch to this rule:
Rule 2:
Sum of Interior Angles = \(180(n-2)\)
(where n = number of sides)
ALL of the interior angles are give to us, so it should be quite easy to find x
Question 3:
a) Find 'x' and hence label all of the interior angles of this pentagon
A line that connects together any two non-consecutive vertices of a polygon is called a diagonal of the polygon. A pentagon will have 5-diagonal
b) Copy out the diagram and draw all 5 diagonals onto your copy
Hints
This time, you have a choice:
You could find the supplementary-angles next to each of the interior-angles
i.e. the exterior-angle next to 5x, would be: 180° - 5x
the exterior-angle next to x+30°, would be: 180° - (x+30°) = 150 - x
Etc
Once you've found ALL of the interior-angles, you can just use RULE 1
The alternative is to find the interior-angles adjacent to each exterior-angle; then use RULE 2
Either way works fine!
Question 4:
a) The sum of interior angles of a polygon is 900°.
i) How many sides does the polygon have?
i) How many diagonals does this polygon have?
b) The sum of interior angles of a polygon is 1440°.
i) How many sides does the polygon have?
ii) How many diagonals does this polygon have?
Hints
PART (a⁞i): ┌───────────────────────────────── ACRONYM: S.o.I.A. = Sum of Interior-angles
┌──┴─┐ ┐
So, we know: SoIA = 900° ├──── SoIA = 180°(n - 2)
n = ??? │ └─┬──┘
┘ 900° = 180°(n - 2)
χ180° χ180°
---------------------
... = n - 2
+2 + 2
--------------------
... = n
Part (a⁞ii): Draw a quick sketch of the polygon (it can be irregular).
Then label the diagonals: A, B, C, D Etc
(I like to label them anti-clockwise
)
Now, draw (say in PINK) diagonals from A to each of the other vertices
(but you can't draw a diagonal from A to B, not from A to the last vertex)
How many diagonals did you draw from A?
Next, move on to B and draw in YELLOW) diagonals from B to each of the other vertices:
Move on to C, drawing the diagonals in GREEN. Now, you'll encounter REPEATS, include them‼
By the time you've finished, you'll have realised THREE things:
⬢ There were ___ vertices (duh!)
⬢ From each vertex, you drew ___ diagonals
⬢ By the end, you had repeated (once) every diagonal
This lead to a system for determining how many diagonals to expect from a polygon with n sides!
𝓒𝓸𝓸𝓵 😎
PART (b):
Sorry, you are on your own with this one, but it is very similar to Part (a)
Question 5:
Up 'til now, all of the polygons we've looked at are CONVEX polygons; but this is a CONCAVE polygon.
You can see that one interior-angle is bigger than 180° (that's called a reflex-angle): So obviously, the corresponding exterior-angle is less than 180°
Another way of comparing CONVEX and CONCAVE polygons is to think about its diagonals:
On a CONVEX polygon, every diagonal will be fully inside the polygon
Print off this polygon and, having worked out \(x\), fill the value of each angle onto your printout
Pick that protactor out of the bin and measure each angle and see if (to the nearest 1°) the angles correspond to your calculations (they should...)
Hints
Again, you've got a choice; you could write in all of the exterior-angles and then use RULE 1
(Be a little careful if you decide to go that direction; because one of the angles is actually negative: It's easy to realise that, if you think back to
the animation and remember the soldier marching in a clockwise direction around the field; at each turn, his instruction was ▢° RIGHT-TURN,
but walking around this field would require ONE ▢° LEFT-TURN, wouldn't it??? Which one??? What angle???)
Or, just write in all of the interior-angles; there's no issue with that method!
3. Regular Polygons:
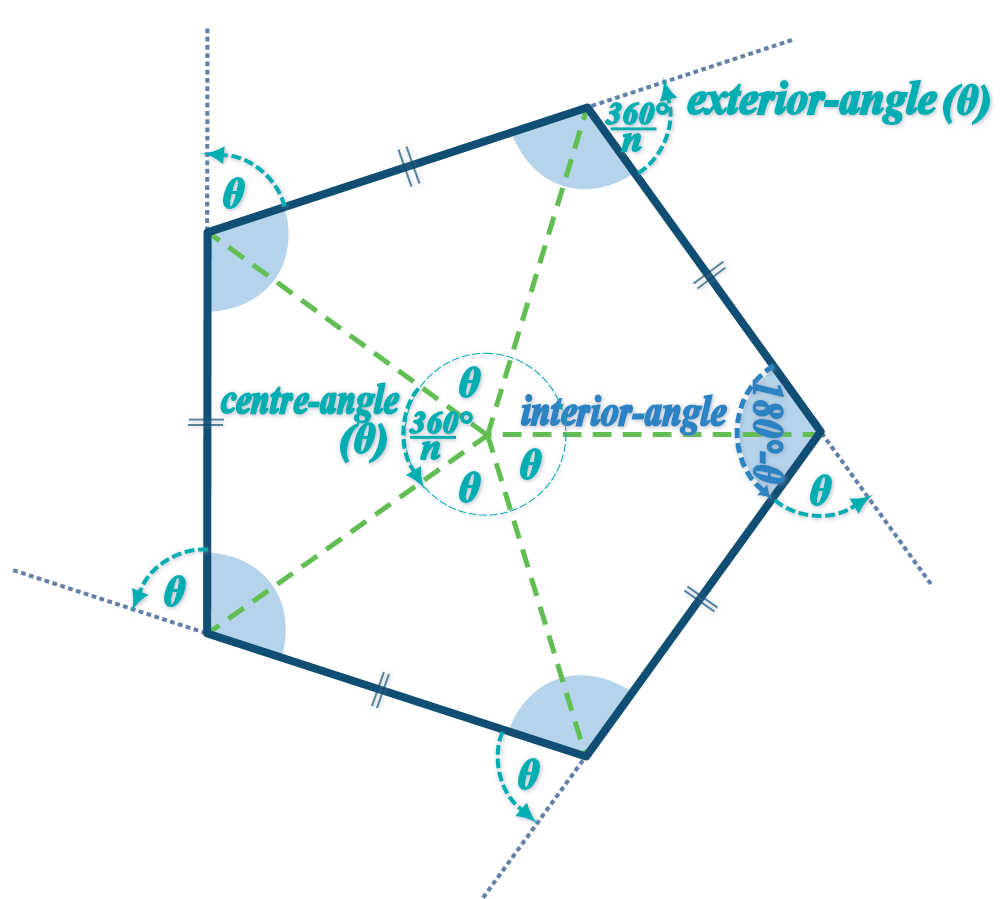
Rule 3:
Centre-angle = \(\theta=\frac{360°}{n}\)
(where n = number of sides)
Rule 4:
Exterior-angle \(\theta\) = Center-angle \(\theta\)
Rule 5:
Interior-angle = \(180-\theta \)
(where \(\theta\) = Exterior-angle)
Note: These rules will work ONLY work for a regular polygon
Question 6:
Find the angles labelled \(x\), \(y\) and \(z\) in this regular pentagon:
Hints
Start by adding in a line, connecting A to O (and also C to O and also D to 0)
and mark in each centre-angle as
°
The centre-angle will be: 360/5 =
°
The exterior angle =
°
The interior angle must be 180° -
° =
°
And the semi-interior-angle is ½(
°) =
°
So, we can say immediately that x =
°
(because it is d--b-e the centre-angle)
Notice that the triangle OBE must be isosceles;
that makes it easy to find y... Finally, since we know angle OBA (the semi-interior-angle of the pentagon) we can subtract y from it to find
Question 7:
Find the angles labelled \(x\), \(y\) and \(z\) in this regular polygon:
Hints
Since this is a regular octagon (8 sides); we know:
The angle at the centre will be: 360/8 =
°
The exterior angle =
°
And the interior angle must be 180° -
° =
°:
So, we can say immediately that x =
°
(because it is an interior angle)
Looking at triangle OED (which is isosceles):
∠EOD =
° (angle at centre)
so: ∠OED =
° (i.e. 180° - 2(
°) )Looking at trapezium ABCD (which is an isosceles trapezium):
∠ABC = ∠BCD =
° and ∠CDA = ∠BAD = y°
But these 4 angles must add up to 360° (interior angles in a quadrilateral add up to 360°):
° +
° + y° + y° = 360°
└─────────┬─────────┘
┌─────┴────┐
° + 2y = 360°
-
° -
°
------------------------
2y =
°
χ2 χ2
------------------
y =
°
Question 8:
a) A regular polygon has interior angle = 165.6°. How many sides does it have?
b) A regular polygon has an exterior angle of 24°. How many sides does it have?
Hints
PART (a):
We are told: Interior-angle = 165.6°
So: Exterior-angle = 180° -
° =
°
Which means: Centre-angle =
°
└────────┬────────┘
│ ┌──────────────────────────────────────────┐
├──────────────┤ But, we know : Angle at Centre = 360°/n │
│ └──────────────────────────────────────────┘
┌─┴─┐
° = 360
n
n = 360°
°
=> n =
An integer, I do hope!
PART (b):
Sadly, I'll have to decline your offer to be helped by me for this part
Question 9:
a) A regular pentagon has sides of 4 cm. What is the area of the pentagon? Could an irregular polygon with the same perimeter have a greater area?
b) A regular octagon is inscribed in a circle of radius 81 cm as shown on the right
Calculate the area inside the circle, but outside the octagon shaded in PINK on the diagram
Hints
PART (b): For a pentagon (n = 5):
Angle at centre = 360/5 = 72°
Exterior Angle = 72°
Interior Angle = 180° - 72° = 108°
We can find the area of the pentagon by first dividing it into 5 isosceles △s
(the "equal" angles in the triangle are half the interior angle)
Extracting one of these, we can split in half to get a right angled triangle:
We can use trigonometry to find the length of the
side opposite the 54° angle:
O= A tan θ
O = 2 tan 54°
O =
cm
To find the area of ONE right angled ◿ use:
Area = ½ base Χ height
Area = ½ base Χ height
= ½(2)(
)
=
cm²
Multiply this by 2 to get the area of the isosceles △
Area of isosceles triangle = 2 Χ
=
cm²
And multiply this by 5 to get the area of the whole pentagon
Area of pentagon = 5 Χ
=
8 cm²
A circle is the shape that gives the largest area for its perimeter and for polygons,
a regular polygon is the closest to a circle.
PART (b):
Sorry - I'm on strike now!
4. To Draw a Regular Polygon (e.g. a pentagon)
The best way to draw accurately a regular polygon is to draw it within a circle:
#1: Use a pair of compasses to draw a large (say 10 cm radius) circle in pencil:

#2: Draw a line from the centre of the circle to the circumference (i.e. 'radius') in pencil:

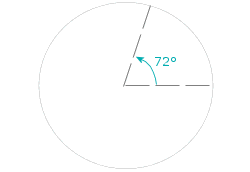
#3: Find the 'Angle at the centre' :
Angle at Centre = 360°
n
In this case, n = 5:
Angle at Centre = 360°
5
= 72°
#4: Draw another radius at 72° (in this case) to the first one:
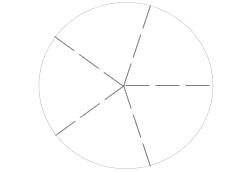
 #5: Repeat until you've gone all the way around the circle:
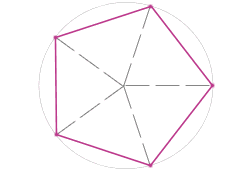
 #6: Connect together the points on circumference with straight lines:
 #7: Finally, rub-out the pencil lines that helped you draw the pentagon:
Question 10: Print off this grid and then draw accurately a regular nonagon using the method described aboveb) Add the triangle shown on the right to your drawing
c) Calculate the sizes of the angles \(a,\,b\) and \(c\), showing clearly your workings
d) Finally, measure those angles using your protractor and see how closely they match the values you calculated they should be...
Hints
You think I'm going to help you with this?
- think again!
Complete this web lesson on separate paper from any other homework
The pass mark (to avoid additional homework on this topic) is: \(\frac{8}{10}\)
Show FULL workings and highlight your answers!!!
|