\(\require{cancel}\)
Web Lesson #27 Indices
› › › Symbol Notation ⇔ Index Notation
INTERACTIVE WEB-LESSON

Completing the Square

The movie shows you REALLY CLEARLY how to Complete-the-Square - that's great; you'll need to use that skill that a lot over the next 3-years...

But the movie doesn't really explain the name: Complete-the-Square? Where is the square, and why does it need completing?

Of course, anyone who likes maths is a Complete-Square, but that's not what we mean here...

Completing-the-Square really means cutting-a-bit-out-of-a-square - so, to explain that, I've set up this Geogebra applet to show you where the square is, and why do we need to cut a piece out of it:

Note: You can edit the constants in the  BLUE  and  RED  boxes
BUT: You'll often need to click TWICE, even when it says "PAUSE"

 

 

Let's check your understanding...

How to Complete the Square

In the first \(6\) questions below - you are doing little more than applying the method shown in the animation:

Question 1
a) Use the method shown in the MOVIE to write \(y\; = \;{x}^{2} \, \color{#bd398c}{+ \,4 }x \, \color{#3C7850}{+ \, 3}\) as a completed square
b) Check that the equation in (a) AND your completed-square give the same value for some abritrary value of \(x\)
c) Use the GEOGEBRA APPLET (above) to produce a diagram which explains your completed square geometrically
Hint
Hints & helpful advice:
	
                ╔═════════════════════════════════════════╗
              ╒═╩═╕                                       ║
       𝑥² + 4𝑥 + 3                                        ║
         ╘═╦═╛                                            ║
    ╒══════╩════════════════════╕                         ║
    │Start by halving the number│        (𝑥    )²         ║
    │in-front of the 𝑥 term and ├—————————————┐           ║
    │put into the brackets:     │        (𝑥 + 2)²         ║
    ╘═══════════════════════════╛                         ║
     Then subtract: (2)²                 (𝑥 + 2)² - (2)²  ║
                                                          ║
     Simplify:                           (𝑥 + 2)² - ...   ║
                                                          ▼
     Now bring down the units term: +3   (𝑥 + 2)² - ... + 3
                                                ╘════╤═════╛
                                                ┌────┴─────┐
                                                │ simplify │
                                                └────┬─────┘
                                                  ╒══╧═══╕
     The answer is:                      (𝑥 + 2)²   -  ...

Checking

The Casio FX991EX (classwiz) can check your ANSWER, so you're sure you got it right (or wrong!)

1) Use your calculator with the equation in the question to find the \(y\)-coordinate at \(x=\) (say) \(1.2\)

⬢ First store \(\color{var(--cyan)}{1.2\rightarrow x}\) on your calculator:

                                   ┌────────── you don't press ALPHA 
                                   │           when STOring 1.2 as X
                                   ▼
On the calculator, TYPE:  1.2    STO    𝑥 

⬢ Then put \(\color{var(--cyan)}{x=1.2}\) into the equation given in the question (i.e. into \(x^2+4x+3\) )

	
TYPE:  𝑥  x²  +  4  𝑥  +  3  = 

2) Next, put \(\color{var(--cyan)}{x=1.2}\) into your completed square (if it's correct, this gives the same \(y\)-value you got in (1) )

	
TYPE:  (  𝑥  +  2  )  x²  -  ⋯  = 

If you wish to understand what's going on here:
In (1) you're putting \(\color{var(--cyan)}{x=1.2}\) into the original equation for \(\color{var(--orange)}{y}\), so that's deffo the correct \(\color{var(--orange)}{y}\)-value at \(\color{var(--cyan)}{x=1.2}\)
In (2), putting the same value (\(\color{var(--cyan)}{x=1.2}\)) into your completed-square
Your completed-square is just a different way of writing original eqn - if correct; \(\color{var(--orange)}{y}\)-values will match!

You can check every completed-square that you do...
...remember; if you ain't checkin', it means you IS chicken

chicken

To show this GEOMETRICALLY, click on the GEOGEBRA applet (above, in the lesson notes) and then edit the constants in the  BLUE  and  RED  boxes

Then keep clicking NEXT (if it says PAUSE but nothing is happening, CLICK-AGAIN)

Then you'll be able to produce a drawing that explains your completed square

Start with the SQUARE with sides  \(\color{var(--fushia)}{x}+\color{var(--midgreen)}{2}\) :

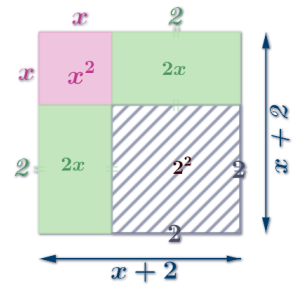
Square diagram

Then show that chopping a square off of one corner is needed:

Why?
Because the striped area (the units term) is \(2^2\) (which is 4) but the units term of \(\color{var(--fushia)}{x^2} + \color{var(--green)}{4x} + \color{var(--midslate)}{3}\) is just \(\color{var(--midlsate)}{3}\)

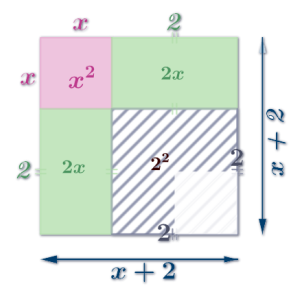
Square with corner removed

...to finally end up with an a square - with a chunk removed (that's what we mean by completed-square), whose AREA is:  \(\color{var(--fushia)}{x^2} + \color{var(--green)}{4x} + \color{var(--midslate)}{3}\)

Question 2
a) Apply the method explained in the movie to write \(y\; = \;{x}^{2} \, \color{#bd398c}{+\,10}x \, \color{#3C7850}{+\,12}\) as a completed square
b) Show the numerical-values that prove that you've checked your completed-square is correct
c) Use the GEOGEBRA APPLET (above) to produce a diagram which explains your completed square geometrically
Hint
Hints & helpful advice:
	 
                  ╔════════════════════════════════════════╗
               ╒══╩═╕                                      ║
       𝑥² + 10𝑥 + 12                                       ║
         ╘═╦══╛                                            ║
    ╒══════╩════════════════════╕                          ║
    │Start by halving the number│        (𝑥    )²          ║
    │in-front of the 𝑥 term and ├—————————————┐            ║
    │put into the brackets:     │        (𝑥 + 5)²          ║
    ╘═══════════════════════════╛                          ║
     Then subtract: (5)²                 (𝑥 + 5)² - (5)²   ║
                                                           ║
     Simplify:                           (𝑥 + 5)² - ...    ║
                                                           ▼
     Now bring down the units term: +12  (𝑥 + 5)² - ... + ...
                                                 ╘════╤══════╛
                                                 ┌────┴─────┐
                                                 │ simplify │
                                                 └────┬─────┘
                                                   ╒══╧═══╕
     The answer is:                      (𝑥 + 5)²   -  ...
	 

Checking

1) Use your calculator with the equation in the question to find the \(y\)-coordinate at \(x=\) (say) \(1.2\)

⬢ First store \(\color{var(--cyan)}{1.2\rightarrow x}\) on your calculator:

                                   ┌────────── you don't press ALPHA 
                                   │           when STOring 1.2 as X
                                   ▼
On the calculator, TYPE:  1.2    STO    𝑥 
	 

⬢ Then put \(\color{var(--cyan)}{x=1.2}\) into the equation given in the question

2) Next, put \(\color{var(--cyan)}{x=1.2}\) into your completed square (if it's correct, this gives the same \(y\)-value you got in (1) )

You can check every completed-square that you do...
...remember; if you ain't checkin', it means you IS chicken

chicken

To show this GEOMETRICALLY, click on the GEOGEBRA applet (above, in the lesson notes) and then edit the constants in the  BLUE  and  RED  boxes

Then keep clicking NEXT (if it says PAUSE but nothing is happening, CLICK-AGAIN)

Then you'll be able to produce a drawing that explains your completed square

Question 3
a) Write \(y\;=\;2{x}^{2}\,\color{#bd398c}{-\,12}x\,\color{#3C7850}{+\,10}\) as a completed square
b) Provide the numerical-values that prove that you've checked your completed-square is correct
Hint
Hints & helpful advice:

Pupils FLOP  this type of question a lot - because the number in-front of the \(x^2\)-term is no longer  ❛ \(\color{var(--mauve)}{1}\) ❜

	 
We cannot complete the square if the coefficient of 𝑥² ≠ 1
                                                 ┌ ┌─────────────┐ ┐
So FIRST, we need to factorise the ‘2’ out:     2│ │ 𝑥² - …𝑥 + … │ │
                                                 └ └──────┬──────┘ ┘
COMPLETE-SQUARE FOR BIT IN BRACKETS    ┌──────────────────┘
                                       │
Halve the coefficient of ‘𝑥’     ┌─────┴─────────────┐ 
and put into the brackets:       │(𝑥 - 3)²           │ 
                                 │                   │ 
Then subtract: (3)²              │(𝑥 - 3)² - (3)²    │ 
                                 │                   │ 
Simplify:                        │(𝑥 - 3)² - ……      │ 
                                 │                   │ 
Then add the units term: +10     │(𝑥 - 3)² - …… + …… │
                                 │                   │ 
Simplify:                        │(𝑥 - 3)²  +  ……    │ 
                                 └─────┬─────────────┘
                                       └──────────────────┐
                                                 ┌ ┌──────┴──────┐ ┐
RE-INSERT INTO THE SQUARE-BRACKETS              2│ │ (𝑥-3)² + …… │ │
                                                 └ └─────────────┘ ┘
                                                │   ▲         ▲
                                                └───┴─────────┘
	 
Finally, multiply out:                           2(𝑥 - 3)² + ……
	 
Question 4
Write  \(y\;=\;3{x}^{2}\,\color{#bd398c}{-\,15}x\,\color{#3C7850}{+\,36}\) as a completed square
I'd advise >checking, but won't force the issue...
Hint
Hints & helpful advice:

Again, the number in-front of the \(x^2\)-term is no longer  ❛ \(\color{var(--mauve)}{1}\) ❜, so we need to adapt:

	 
We cannot complete the square if the coefficient of 𝑥² ≠ 1
                                                 ┌ ┌─────────────┐ ┐
So FIRST, we need to factorise the ‘3’ out:     3│ │ 𝑥² - …𝑥 + … │ │
                                                 └ └──────┬──────┘ ┘
COMPLETE-SQUARE FOR BIT IN BRACKETS    ┌──────────────────┘
                                       │
Halve the coefficient of ‘𝑥’     ┌─────┴─────────────┐ 
and put into the brackets:       │(𝑥 - …)²           │ 
                                 │                   │ 
Then subtract: (…)²              │(𝑥 - …)² - (…)²    │ 
                                 │                   │ 
Simplify:                        │(𝑥 - …)² - ……      │ 
                                 │                   │ 
Then add the units term: +12     │(𝑥 - …)² - …… + …… │
                                 │                   │ 
Simplify:                        │(𝑥 - …)²  +  ……    │ 
                                 └─────┬─────────────┘
                                       └──────────────────┐
                                                 ┌ ┌──────┴──────┐ ┐
RE-INSERT INTO THE SQUARE-BRACKETS              3│ │ (𝑥-…)² + …… │ │
                                                 └ └─────────────┘ ┘
                                                │   ▲         ▲
                                                └───┴─────────┘
	 
Finally, multiply out:                           3(𝑥 - …)² + ……
Question 5
Write \(y\;=\;4{x}^{2}\,\color{#bd398c}{+\,2}x\,\color{#3C7850}{-\,8}\) as a completed square
Hint
Hints & helpful advice:
	 
We cannot complete the square if the coefficient of 𝑥² ≠ 1
                                                 ┌ ┌─────────────┐ ┐
So FIRST, we need to factorise the ‘4’ out:     4│ │ 𝑥² + …𝑥 - … │ │
                                                 └ └──────┬──────┘ ┘
COMPLETE-SQUARE FOR BIT IN BRACKETS    ┌──────────────────┘
                                       │
Halve the coefficient of ‘𝑥’     ┌─────┴─────────────┐ 
and put into the brackets:       │(𝑥 + …)²           │ 
                                 │                   │ 
Then subtract: (…)²              │(𝑥 + …)² - (…)²    │ 
                                 │                   │ 
Simplify:                        │(𝑥 + …)² - ……      │ 
                                 │                   │ 
Then add the units term: +……     │(𝑥 + …)² - …… - …… │
                                 │                   │ 
Simplify:                        │(𝑥 + …)²  -  ……    │ 
                                 └─────┬─────────────┘
                                       └──────────────────┐
                                                 ┌ ┌──────┴──────┐ ┐
RE-INSERT INTO THE SQUARE-BRACKETS              4│ │ (𝑥+…)² - …… │ │
                                                 └ └─────────────┘ ┘
                                                │   ▲         ▲
                                                └───┴─────────┘
	 
Finally, multiply out:                           4(𝑥 + …)² - …… 
	 
Question 6
Write \(y\; = \;\frac{1}{2}{x}^{2}\,\color{#bd398c}{+\,2}x \,\color{#3C7850}{+\,6}\) as a completed square
Hint
Hints & helpful advice:
	 
We cannot complete the square if the coefficient of 𝑥² ≠ 1
                                                 ┌ ┌──────────────┐ ┐
So FIRST, we need to factorise the ‘½’ out:    ½  │ │ 𝑥² + 4 𝑥 + 12   │ │
                                                 └ └──────┬───────┘ ┘
COMPLETE-SQUARE FOR BIT IN BRACKETS    ┌──────────────────┘
                                       │
Halve the coefficient of ‘𝑥’     ┌─────┴─────────────┐ 
and put into the brackets:       │(𝑥 + …)²           │ 
                                 │                   │ 
Then subtract: (…)²              │(𝑥 + …)² - (…)²    │ 
                                 │                   │ 
Simplify:                        │(𝑥 + …)² - ……      │ 
                                 │                   │ 
Then add the units term: +……     │(𝑥 + …)² - …… + 12 │
                                 │                   │ 
Simplify:                        │(𝑥 + …)²  +  ……    │ 
                                 └─────┬─────────────┘
                                       └──────────────────┐
                                                 ┌ ┌──────┴──────┐ ┐
RE-INSERT INTO THE SQUARE-BRACKETS             ½  │ │ (𝑥+…)² + …… │ │
                                                 └ └─────────────┘ ┘
                                                │   ▲         ▲
                                                └───┴─────────┘
	 
Finally, multiply out:                           ½(𝑥 + …)² + …… 
	 
Uses of the Completed Square

If you try putting various different numbers into the equation:  \(y=x^2+4x-6\)

You will not be able to get an answer below:  \(-10\)

Let's try it and see...

\(x\)
\(y\)
\(-7\)
\(15\)
\(-6\)
\(6\)
\(-5\)
\(-1\)
\(-4\)
\(-6\)
\(-3\)
\(-9\)
\(-2\)
\(-10\)
\(-1\)
\(-9\)
\(0\)
\(-6\)
\(1\)
\(-1\)
\(2\)
\(6\)
\(3\)
\(15\)

Now, if I write the same equation in ‘completed square’-form:

\(y=\left( x+2 \right) ^2\,\color{#3C7850}{-\,10}\)

It starts to become obvious why:

  • When we put a number into this equation, we first ‘add \(2\)’
  • Then we square it
  • Then we subtract ‘\(10\)’

It's the ‘square it’ step that makes the function have a minimum of ‘\(-10\)’

The reason is that, when you square a number (even a negative number); the answer is always positive (or zero!)

So, the lowest \({\left(x-1\right)}^{2}\) can be is:  \(0\) (if we put in \(x\,=\,-2\))

So, the lowest \({\left(x+2\right)}^{2}\,\color{var(--green)}{-\,10}\) can be is \(-10\)  (if we put \(x\,=\,-2\))

Question 7
Find the minimum value of \(y\;=\;{\left(x-1\right)}^{2}\,\color{#3C7850}{+\,5}\)
Hint
Hints & helpful advice:
	 
What is the lowest that (𝑥-1)² can be?     The answer is: ❛ 0 ❜ (You know why, dontcha?)
 
So, what is the lowest that (𝑥-1)² + 5 can be? 
 
If you're in any way confused about this - try filling in this table:

     𝑥     │  -3    -2    -1     0     1     2     3     4
  ─────────┼─────────────────────────────────────────────────
  (𝑥-1)²   │  16     9     4     …     …     …     …     … 
  ─────────┼─────────────────────────────────────────────────
(𝑥-1)² + 5 │  21     14    …     …     …     …     …     …

Identify the column that gives the smallest value of \((x-1)^2\) \(+\,5\)

Work back up that column and consider why that value of \(x\) gives the minimum value of: \((x-1)^2\) \(+\,5\)

Question 8
Find the minimum value of: \(y\;=\;{x}^{2}\,\color{#bd398c}{+\,6}x\,\color{#3C7850}{-\,5}\)
What value of \(x\) gives this minimum value of \(y\)?
Hint
Hints & helpful advice:
Sorry - you're on your own with this one - but start by completing the square - obviously!
	 
Question 9
Find the minimum value of \(y\;=\;2{x}^{2}\,-\,4x\,+\,18\)
Hint
Hints & helpful advice:
	
We need to complete the square first: y = 2(𝑥 - 1)² + ...
 
What is the lowest that (𝑥-1)² can be?
 
So, what is the lowest that (𝑥-1)² + ... can be?
Question 10
Find the minimum value of \(y\;=\;\frac{1}{4}{x}^{2}\,-\,\frac{1}{2}x\,+\,1\). What value of \(x\) gives this minimum value of \(y\)?
Hint
Hints & helpful advice:
	 
Factorising the Ό   out is where an error is likely
	 
We cannot complete the square if the coefficient of 𝑥² ≠ 1
                                                 ┌ ┌──────────────┐ ┐
So FIRST, we need to factorise the ‘Ό’ out:    Ό  │ │ 𝑥² - 2 𝑥 +  4    │ │
                                                 └ └──────┬───────┘ ┘
COMPLETE-SQUARE FOR BIT IN BRACKETS    ┌──────────────────┘
                                       │
                                 ┌─────┴─────────┐ 
                                 │(𝑥 - …)²  +  … │ 
                                 └─────┬─────────┘
                                       └──────────────────┐
                                                 ┌ ┌──────┴──────┐ ┐
RE-INSERT INTO THE SQUARE-BRACKETS             Ό  │ │ (𝑥-…)² + …… │ │
                                                 └ └─────────────┘ ┘

Multiply out the  Ό       and figure out how to find the minimium-value...

Complete this web-lesson on separate paper from other homework

The pass mark (to avoid additional hmk on this topic) is:  \(\frac{8}{10}\) 

Show FULL workings and  highlight your answers