Page 61, Column 1

Surface Areas

The "NET" of a shape helps us to determine its surface area. The "NET" is the shapes of paper we would need in order to fold/roll and stick together to create the 3-dimensional object

 

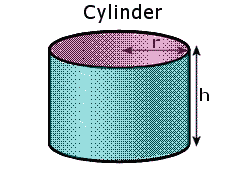
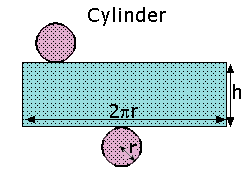
Cylinders

The net of a cylinder is made up of two small circles and a long rectangle:

The two circles form the base and lid of the cylinder and the rectangle forms the curved surface of the cylinder:

  1. The height of the cylinder is called 'h' and the radius of the base is called 'r'

  2. Cylinders are similar in shape if they have the same ratio of 'h/r'

  3. The circumference of the small circle must equal the width of the rectangle

  4. The area of the curved surface of the cylinder (Ac) is given by '2лrh'

  5. The total surface area, S = 2лrh + 2лr²

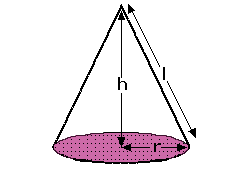
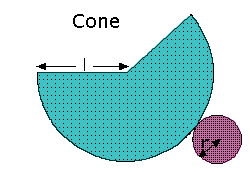
  e.g. A cylinder has height 4 cm and base radius 3 cm. Find its surface area 
  h = 4cm  ┐
  r = 3 cm |
  S = ???  ┘		S  =	2лrh     +  2лr²
			   = 	2л(3)(4) +  2л(3)² 
			   =	42л cm²
e.g. A cylinder of height 6 cm has surface area of 32л cm². Find its base radius 
  h = 6 cm    ┐
  r = ???     |
  S = 32л cm² ┘		S   =	2лrh   +  2лr²
			32л =	2лr(6) +  2лr²
			32л =  12лr    +  2лr²
			÷2л    ÷2л       ÷2л
			----------------------
			16  =   6r     +  r²
			-16                  -16
			------------------------
			  0 =   r²  +  6r  -  16

		    =>	  0 = (r + 8)(r - 2)
		    =>	  r = -8 or r = 2

Cones

The net of a cone is made up of a small circle and a sector of a large circle:

The full circle forms the base of the cone and the sector forms the curved surface of the cone:

  1. The perpendicular height of the cone is called 'h', whereas the slant height is called 'l'. Together with the radius of the base, these three lengths form a right angled triangle.

  2. 'θ' is called the 'semi-vertical angle' of the cone. Cones which have the same semi-vertical angle are similar in shape.

  3. The arc of the sector must equal the circumference of the small circle

  4. The area of the sector (Ac) is given by 'лrl'

  5. The total surface area, S = лrl + лr²

e.g. A cone has height 4 cm and base radius 3 cm. Find its surface area 
  h = 4     ┐
  r = 3     |
  l = ???   | 			We need 'l' :        l²	= h² + r²
  A = ???   ┘ 			(the slant height)   l²	= 4² + 3²
						     l 	= 5 cm
 
				Area of curved surface	= лrl
				(i.e. sector of net) 	= л(3)(5)
							= 15л cm²
 
				Area of base of cone 	= лr²
							= л(3)²
							= 9л cm²
 
				Total area 	= 15л + 9л
						= 24л cm²

Volume of a Sphere

Sphere
 
   Volume  = 4 л r³
             3
e.g. A sphere has radius 2 cm. Find its volume
  r = 2    ┐
  V = ???  ┘			V  =  4лr²
				      3 
 
				   =  4л(2)²
				      3 
 
				   =  16л cm²
				       3

Surface area of a Sphere

The net for a sphere is impossible to flatten out - but it looks a bit like this:

Net of a Sphere
 
 Surface Area = 4 л r²
e.g. A sphere has radius 2 cm. Find its surface area
  r = 2    ┐
  S = ???  ┘			S  =  4лr²
				   =  4л(2)²
				   =  16л cm²

Question 1: The volume is given by: 

  r = 3    ┐
  V = ???  ┘			V  =  4лr²
				      3 
 
				   =  4л(3)²
				      3 
 
				   =  ...л cm²

Question 7: A hemisphere is HALF a sphere, so we work out the volume of a whole sphere - then halve it...

 

Question 8: Working out the volume of a sphere of radius 1.2 cm and multiplying that by 20 givens the volume of the cuboid...

 

Question 10 part (a): It is easy to use Pythag to work out the hypotenuse (i.e. slant height)
 

Question 10, part (b): Separating the object into a cone and a hemisphere:

The net for a cone (excluding the base circle of the cone) is: 
Curved Surface of a Cone
 
 Surface Area = л r l

The net of a hemisphere is: 
Net of a Hemisphere
 
 Surface Area = 4 л r²
                  2

 

Question 12: The net for a cone (excluding the base circle of the cone) is: 
Curved Surface of a Cone
 
 Surface Area = л r l

The net of the cylinder (open toped and open bottomed) is: 
 
Curved Surface
of a Cylinder
 
 Surface Area = 2 л r h

 

Question 17: It doesn't matter is the pencil has a circular cross section, or a triangular cross section of e hexagonal cross section...

...the end of a pencil is a type of "pyramid", so the same formula applies: A = 1/3 × area of base × height

 

Question 19: So, we can work out the volume of the sphere: V = ... cm³

Since the cylinder has the same volume:

				Volume of cylinder =  лr²h
				                       │ └┐
					       ... = л(…)²h
						÷…      ÷…
					       ------------
						…  =      h

Question 20: Since height is twice radius:

				 height  is  twice  radius
				╘═══╤══╛╘═╤╛╘══╤══╛╘═══╤══╛
				    h     =    2×      r

And, using the equation for the volume of a cylinder:

				Volume of cylinder =  лr²h
				                │      │ └┐
					       ... =  лr²(2r)

Solving...