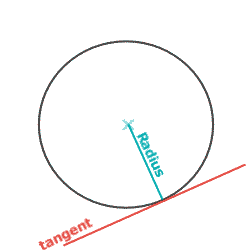
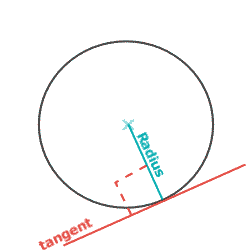
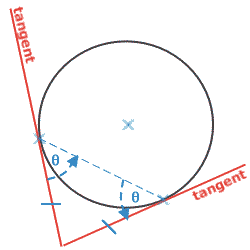
Page 43, Column 1

Angles: Circle Rules

There are 8 rules altogether

The first 5 were covered on Pages 41 & 42

The last 3 rules are covered here:

Rule 6: "Radius meets Tangent"

The angle between a radius and a tangent must be 90°:

A radius passes through the centre of
the circle. A tangent touches the circle
(i.e. doesn't cut through the circle):
    

——►——

When a radius meets a tangent, the angle
between them must by 90°

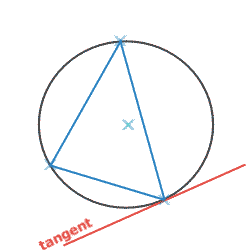
Rule 7: Triangle meets Tangent

Called the Triangle Tangent Theorem (or the Alternate Segment Theorem)

When a triangle (with all three vertices on the circumference) meets a tangent; the opposite angles will be equal:

If a cyclic triangle (i.e. with all 3
vertices on the circumference) meets
a tangent:
    

——►——
 
 
 
 
 
 
 
 
 

 
 
 
 
 
 
 
 
——►——

 
Then the opposite angles are equal: 
 
 
 
 
╔══════════►
║
║
║
║
║
║
║
╠═════════► 
║
║ 
╚════ So, these two angles are equal 

and these two angles are also equal:
          ║             ║
          ║             ║
          ║             ║
          ║             ║
          ║             ║
          ║             ║
          ║             ║
          ▼             ║
                        ▼
 
 
 
 
 
 
 

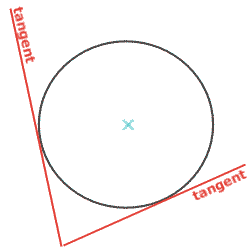
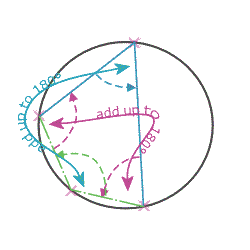
Rule 8: Two Tangent Rule

When two tangents to the same circle meet, an isosceles triangle can be formed:

Two tangents to the same circle meet:
    

——►——

Producing an ISOSCELES triangle:

Question 2: This is a CYCLIC QUADRILATERAL. Using RULE 4:

So: s = ...° and the angle opposite the 110° = ...°

Finally, using 'angles on a line' to find: r = ...° 

Note: At each stage you must state a reason (in words) for your answer: Like this:
s = ... (cyclic quadrilateral - opposite angles sum to 180°)
angle opposite 110° is ...° (cyclic quadrilateral - opposite angles sum to 180°)
r = ... (half turn rule)

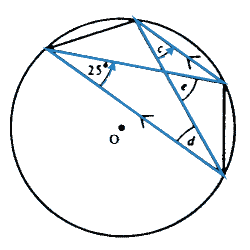
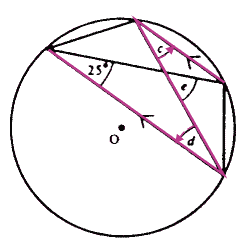
Question 4: Using RULE 1:

So: c = ...°

Using the 'Z-rule' (parallel lines: alternate angles):

So: d = ...°

Using 'angles in a triangle' and then 'angles on a line': e = ...°

Note: At each stage you must state a reason (in words) for your answer

Question 5: Using RULE 4: h = 2 × ...°

And, since the triangle is isosceles ...

Note: At each stage you must state a reason (in words) for your answer

Question 6: Using the U-rule: l = ...°

Using RULE 2: l =  2 × ...
So: m = ...°

Using RULE 4 ...

Note: At each stage you must state a reason (in words) for your answer

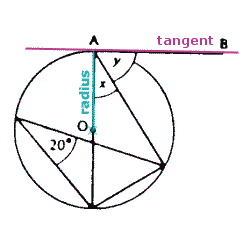
Question 10: Using RULE 1: x = ...°

Using RULE 6: (Radius meets tangent at ...°)

angle OAB = 90° so angle y = ...°

Note: At each stage you must state a reason (in words) for your answer

Question 11: Using RULE 2: x = ...°

Using RULE 6: angle OAB = 90° so angle y = ...°

Note: At each stage you must state a reason (in words) for your answer

Question 12: Using RULE 6; angle OAB = 90° so we can use Pythagoras' Theorem to find the length AB

Note: At each stage you must state a reason (in words) for your answer

Question 15: Divide the "right trapezium" into a rectangle and a triangle and then use Pythagoras' Theorem to find OC

Note: At each stage you must state a reason (in words) for your answer