Page 40, Column 2Polygons1. Naming Polygons
The number of sides is usually referred to as 'n'
|
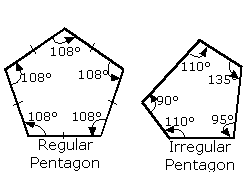
Regular PolygonsFor a regular polygon, all their angles are the same as each other and all of the lengths are the same as each other |
Some of the rules below apply to ALL polygons (regular or irregular). Other rules only apply to regular polygons...
3. All Polygons (Regular & Irregular):

Rule 1:Sum of Interior Angles = 180(n-2) |
e.g. For a Triangle:
Sum of the interior angles = 180(3-2) = 180°
e.g. For a Quadrilateral:
Sum of the interior angles = 180(4-2) = 360°
e.g. For a Pentagon:
Sum of the interior angles = 180(5-2) = 540°
e.g. Find the missing exterior angle in this polygon
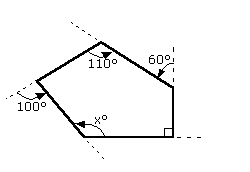
First of all, we have to write in all of the interior angles
The angle at the left (100°) is an exterior angle. The interior angle corresponding to this is '180°-100°' = 80°
Similarly, the interior angle on the right is 120°. So our polygon looks like this:
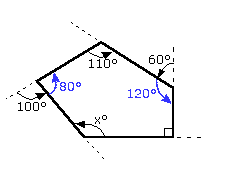
Now, since the number of sides ('n') = 5:
Sum of Interior Angles = 180(5-2) = 540 So: 80° + 110° + 120° + 90° + x = 540° 400° + x = 540° => x = 140°
e.g. Find 'x' and hence label all of the interior angles in this polygon
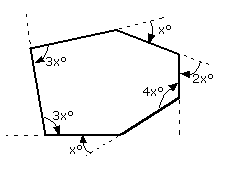
Again, we start by finding all of the interior angles:
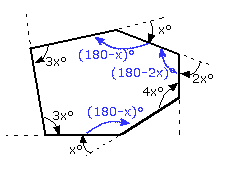
Now, since the number of sides ('n') = 6:
Sum of Interior Angles = 180(6-2) = 720° 3x° + (180-x)° + (180-2x)° + 4x° + (180-x)° + 3x = 720° => 540° + 3x = 720° => x = 30°
So the interior angles are (starting from the top left and working anticlockwise): 90°, 90°, 150°, 120°, 120°, 150°.
e.g. A polygons interior angles add up to 2520°. How many sides does it have?
Since:
Sum of Interior Angles = 180(n-2) => 2520 = 180(n-2) => 16 = n
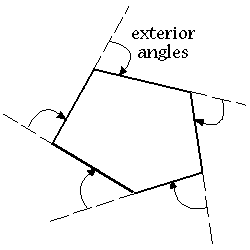
Rule 2:Sum of Exterior Angles = 360° |
Note: Rules 1 & 2 will work for any polygon; regular or irregular
e.g. Find the missing angle in this polygon

This time, we need to find all of the 'exterior' angles. The exterior angle corresponding to the 110° angle at the top is '180°-110°' = 70° etc...
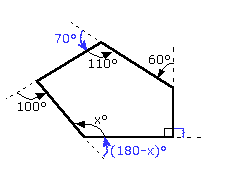
And, since the sum of the exterior angles must equal 360°:
Sum of Exterior Angles = 360° 70° + 100° + (180-x)° + 90° + 60° = 360° => 500 - x = 360 => x = 140°
e.g. Find 'x' and hence label all of the exterior angles in this polygon

Again, we need to find all of the exterior angles:
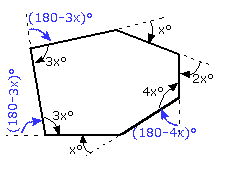
And since the sum of the exterior angles is 360°:
Sum of Exterior Angles = 360° (180-3x)° + (180-3x)° + x° + (180-4x)° + 2x° + x° = 360 => 540 - 6x = 360 => x = 30°
So the exterior angles are (starting from the top left and working anticlockwise): 90°, 90°, 30°, 60°, 60°, 30°
4. Regular Polygons:
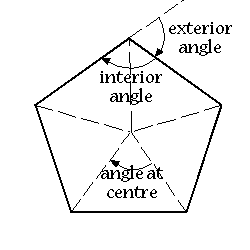
Rule 3:Angle at the Centre = 360°/n Rule 4:Exterior Angle = Angle at Centre Rule 5:Interior Angle = 180° - Exterior Angle |
Note: These rules will work ONLY work for a regular polygon
e.g. Sketch a heptagon and label all of the angles (angle at centre, interior angle and exterior angle
The angle at the centre is: 360/7 = 51.4°
So the exterior angle is: 51.4°
Which means the interior angle is: 180 -
51.4 = 128.6°
e.g. Find the angles labelled 'x' and 'y' in this regular polygon:
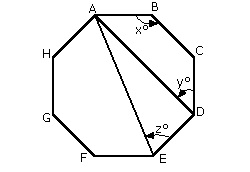
Since this is a regular octagon; we know the angle at the centre must be 360/8 = 45°
So therefore, the exterior angle must also be 45°
And the interior angle must be 180° - 45° = 135°:
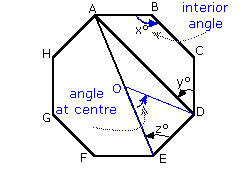
So, we can say immediately that x = 135° (because it is an interior angle)
Looking at triangle OED (which is isosceles). ÐEOD = 45° (angle at centre). So ÐOED = 67.5°
Looking at the trapezium ABCD (which is an isosceles trapezium): ÐABC = ÐBCD = 135°. And ÐCDA = ÐBAD = y°
But these 4 angles must add up to 360 (angles in a quadrilateral add up to 360°):
Sum of Interior Angles = 180(4-2) = 360° 135° + 135° + y° + y° = 360 => 270 + 2y = 360 => y = 45°
e.g. A regular polygon has interior angle = 165.6°. How many sides does it have?
So, exterior angle = angle at centre = 180° - 165.6° = 14.4°
And since: Angle at Centre = 360° n 14.4 = 360° n => n = 25
e.g. A regular pentagon has sides of 4cm. What is the area of the pentagon. Could an irregular polygon with the same perimeter have a greater area?
We can find the area of the pentagon by first dividing it
into 5 isosceles triangles
Extracting one of these, we can split in half to get a right
angled triangle:
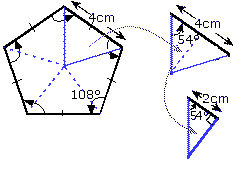
We can find the side opposite the 54° angle using trigonometry:
╖ A = 2 cm ║ O = A tan θ O = ? ║ O = 2 tan 54° θ = 54° ║ O = 2.753 cm ╜
And then use Area = ½ × base × height to find the area of the right angled triangle:
Area = ½ × base × height Area = ½ × 2 × 2.753 Area = 2.753 cm²
Multiply this by '2' to get the area of the isosceles triangle:
Area of isosceles triangle = 5.51 cm²
And multiply this by '5' to get the area of the pentagon:
Area of Pentagon = 27.5 cm²
A circle is the shape that gives the largest area for its perimeter and for polygons, a regular polygon is the closest to a circle. So the answer is 'NO' an irregular polygon with the same perimeter could not have a greater area
5. To Draw a Regular Polygon (e.g. a pentagon)
The best way to draw accurately a regular polygon is to draw it within a circle:
-
Start by drawing a circle in pencil
-
Draw a line from the centre of the circle to the circumference (called a 'radius') in pencil
-
Find the 'Angle at the centre'
Angle at Centre = 360°/n [in this case: 360°/5 = 72°] -
Draw another radius at 72° (in this case) to the first one
-
Repeat until you've gone all the way around the circle
-
Using a pen, connect together these points on circumference with straight lines to form your pentagon
-
Rub out the pencil lines which helped you to draw the pentagon
Question 1: Using RULE 2: Sum of exterior angles = 360°
Sum of exterior angles = 360° 90° + 85° + 65° + p + 90° = 360° p = ...
Question 2: Again, we are going to use the RULE 2: Sum of exterior angles = 360°
But one of the angles (115°) is an interior angle
If we extend the horizontal line to the left, then the exterior angle can be found as '180 - 115' = 65°
Sum of exterior angles = 360° 65° + ...° + ...° + p + ...° = 360° p = ...°
Question 3: Still using RULE 2:
Sum of exterior angles = 360° ...° + 2x + x + 2x = 360° x = ...
Question 6: We know from RULE 4 that:
Exterior Angle = Angle at Centre 72° = Angle at Centre
And, we know from RULE 3 that:
Angle at Centre = 360 n 72° = 360 n
Solving...
Alternative Method: Imagine there are 'n' sides to this polygon. Since
the sum of the interior angles must equal 360°:
72n = 360°
So n = ...
Question 7: Using RULE 1, for a polygon with 5 sides:
Sum of Interior Angles = 180(5-2) = 540° x + 2x + 3x + 3x + x = 540° x = ...
Question 12: We want to use RULE 1 (for a polygon with 4 sides):
Sum of Interior Angles = 180(4-2) = 360°
BUT, one of these angles (‘x’) is an exterior angle...
We can find the interior angle at that point using RULE 5:
Interior Angle = 180 - Exterior Angle Interior Angle = 180 - x
Now, using RULE 1 as described above:
Sum of Interior Angles = 180(4-2) = 360° ...° + ...° + ...° + 180-x = 360° x = ...
Question 13: Again, we need to find the two interior angles, where we have been given exterior angles...
And then use RULE 1 (for a polygon with 5 sides):
Sum of Interior Angles = 180(5-2) = 540°