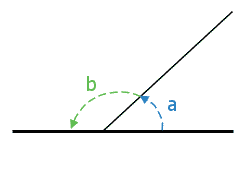
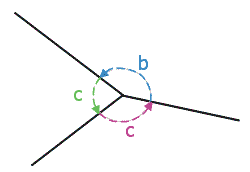
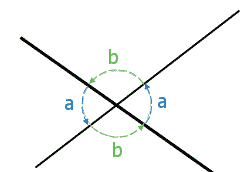
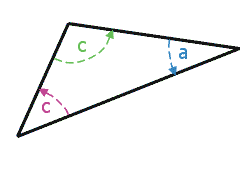
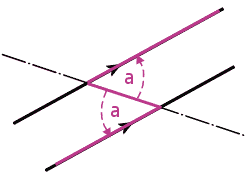
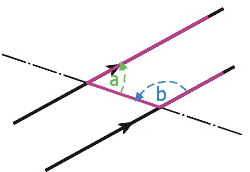
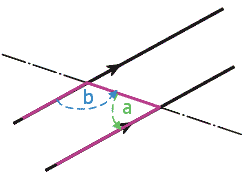
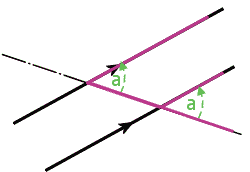
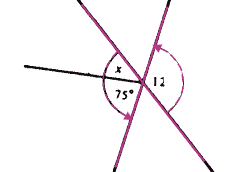Page 39, Column 2

Angle Rules:

  1. Lines:

    (i) Half Turn Rule...
    ...add up to 180°
     
    (ii) Full Turn Rule...
    ...add up to 360°
     
    (iii) Intersecting lines...
    ...vertically opposite angles are equal

  2. Angles in a Triangle:

    (i) Any triangle...
    ...angles add up to 180°
     
     
    (ii) Isosceles triangles...
    ...have two angles the same
    (and two lengths the same)
      
    (iii) Equilateral triangles...
    ...have all three angles the same (i.e. 60°) and all three lengths are the same

  3. Parallel Lines: Z-rule

    Parallel lines can produce the Z-rule

     
    (i) Z-rule: Angles in the elbows of the ‘Z’ are equal:
    ...alternate angles are equal
    (ii) Z-rule: The 'Z' can be drawn the other way around:
    ...alternate angles are equal

  4. Parallel Lines: U-rule

    Parallel lines can also produce the U-rule

     
    (i) U-rule: Angles in the bends of the ‘U’ add up to 180°
    ...allied angles add up to 180°
    (ii) U-rule: The ‘U’ can also be drawn upside down
    ...allied angles add up to 180°

  5. Parallel Lines: F-rule

    Parallel lines can also produce the F-rule
    (i) F-rule: Angles under each arm of the ‘F’ are equal
    ...corresponding angles are equal
    (ii) F-rule: A mirrored ‘F’ can be used as well
    ...corresponding angles are equal

 

Referring to the Rules

It is important to use the correct description when using these rules:

  • When using the Z-rule, state, "Parallel Lines: Alternate Angles" 
  • When using the U-rule, state, "Parallel Lines: Allied Angles"
  • When using the F-rule, state, "Parallel Lines: Corresponding Angles" 

 

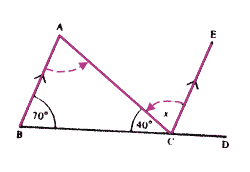
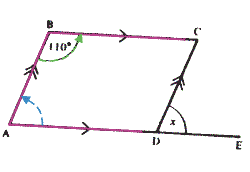
Question 1: First, use "Angles in a Triangle Add up to 180°" to find the angle at ‘A’...

The use the Z-rule to find ‘x’:

Finally, using "Angles on a Straight Line Add up to 180°" (at C) gives ΠDCE = 180° – ... – ... = …

Note: When using the Z-rule, you must state "parallel lines: alternate angles"

 

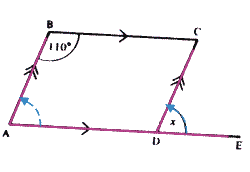
Question 2: We can find the answer in 1 go, using the Z-rule:

Note: When using the Z-rule, you must state "parallel lines: alternate angles"

 

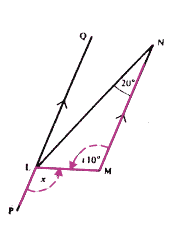
Question 3: Use "Angles on a Line Add up to 180°" to find ΠSQT

Then use the Z-rule...

Alternatively, use the "Intersecting Lines" rule gives ΠUQR as 120° and then use the U-rule

 

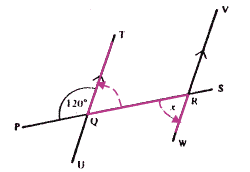
Question 4: Using the U-rule gives ΠBAD

Note: When using the U-rule, you must state "parallel lines: allied angles"

Then, using the F-rule gives x

Note: When using the F-rule, you must state "parallel lines: corresponding angles"

 

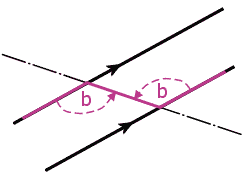
Question 5: Ignore the short line (that doesn’t go through the intersection) and using "Intersecting Lines":

So we know that: 120° = x+75°

 

Question 7: Using the rule, "Angles Around a Point Add up to 360°":

So: 110 + x + x = 180

 

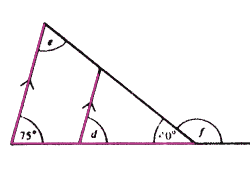
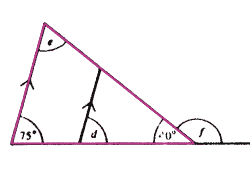
Question 9: ‘d’ can be found using the F-rule:

Note: When using the F-rule, you must state "parallel lines: corresponding angles"

‘e’ can be found using the "Angles in the large Triangle":

‘f’ can be found using the "Angles on a Straight Line" rule

 

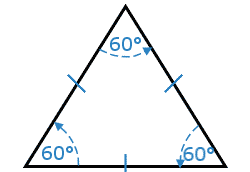
Question 10: Notice the triangle has 3 sides that are the same length (equilateral). That means all three angles are equal and, since they must add up to 180°, they must all be 60° (we know this anyway, using the rule: "Angles in an Equilateral Triangle are all 60°")

 

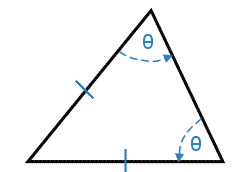
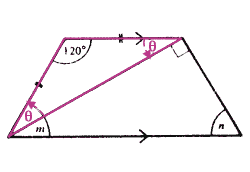
Question 11: Notice the triangle has 2 sides that are the same length (isosceles). That means two of angles (i.e. the one they've labelled ‘k’ and the one they've labelled ‘l’) are actually equal - so I've labelled them both as ‘θ’ 

and, since they must add up to 180°: θ + θ + 120 = 180°