|
2 The Scale Factor Method Case #1 of 10
∙01 Direction Proportion
Scale Factor Method #1Two quantities, such as the mass of apples and the price of the apples are obviously related to each other. In fact, they are in direct proportion to one another, because: 1. Buying more apples would cost more money2. Double the mass of apples would normally cost twice as much (if no bulk-buying discounts)Whenever two quantities are in direct proportion we can use the scale factor method: e.g. 2.5 kg of apples cost £1.20. How much would 4.75 kg of apples cost?Step 1: We know that 2.5 kg of apples costs £1.20, so we write this first:
MASS COST
---------------------------
2.5 kg ► £1.20
Step 2: We want to find the cost of 4.75 kg, so we write 4.75 kg under the 2.5 kg:
MASS COST
---------------------------
2.5 kg ► £1.20
4.75 kg ► _____
▲ ┌────────────────┐
└───────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { 4.75 }{ 2.5 }\) (i.e. the number at the bottom divided by the number at the top):
MASS COST
---------------------------
┌ 2.5 kg ► £1.20
Χ4.75 │
2.5 │
└►4.75 kg ► _____
Step 4: The SAME Scale-factor (\(\times \frac { 4.75 }{ 2.5 }\)) will also convert the £1.20:
MASS COST
---------------------------
┌ 2.5 kg ► £1.20 ─┐
Χ4.75 │ │ Χ4.75
2.5 │ │ 2.5
└►4.75 kg ► _____ ◄┘
Step 5: So the answer is: \( £1.20\;\times\; \frac { \color{yellowgreen}{4.75} }{ \color{cornflowerblue}{2.5} } \;=\; \color{mediumvioletred}{£2.28} \) ·Some question will require you to convert hours, minutes and second into hours (or perhaps into minutes). Although is should be obvious that 2.5 hours is the same as 2 hours, 30 minutes (NOT: 2 hours 50 minutes!), it is still easy to make a mistake with that This comes under the heading Denominate Numbers - but the calculator can help you with that:e.g. Convert: 2 hours, 25 minutes and 12 seconds into HOURS:The calculator can easily do this: Press:2°"25°"12°"=.Finally, press:°"once more· ·We can adapt the method for a slightly harder situation: If, as the first quantity increases, the rate at which the second quantity increases changes... Expressed in that abstract way, that is hard to understand - but a situation makes it easy to understand: And we can easily adapt our method to deal with that: e.g. Panasonic make two identical OLED TVs, one with screen size 42-inches priced at £600 and another with screen-size 63-inches. How much should I expect to pay if price is proportional to square of screen size?Step 1: We know that 2.5 kg of apples costs £1.20, so we write this first:
SIZE² PRICE
-----------------------------
42² inch² ► £600
└─┬─┘ ┌───────────────────────────────┐
└────────────────────────────────┤ Price depends on Screen-size² │
│ So, we must SQUARE the sizes │
└───────────────────────────────┘
Step 2: We want to find the cost of a 63 inch TV, so we write 63² inch² under the 42² inch²:
SIZE² PRICE
-----------------------------
42² inch² ► £600
63² inch² ► _____
▲ ┌────────────────┐
└───────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { {63}^{2} }{ {42}^{2} }\) (i.e. the number at the bottom divided by the number at the top):
SIZE² PRICE
-----------------------------
┌ 42² inch² ► £600
Χ63² │
42² │
└►63² inch² ► _____
Step 4: The SAME Scale-factor (\(\times \frac { {63}^{2} }{ {42}^{2} }\)) will also convert the £600:
SIZE² PRICE
-----------------------------
┌ 42² inch² ► £600 ─┐
Χ63² │ │ Χ63²
42² │ │ 42²
└►63² inch² ► _____◄┘
Step 5: So the answer is: \( £600\;\times\; \frac { \color{yellowgreen}{ {63}^{2} } }{ \color{cornflowerblue}{ {42}^{2} } } \;=\; \color{mediumvioletred}{£1350} \) ·Question 1: What a generous shopkeeper - he's willing to break the pack and sell the pens individually to me. ? Oh, but how ever many I buy, he's gonna charge me \(£1.80\) extra just for breaking the pack - what a mean and grumpy old slouch! Step 1: We know that the pack of 12 pens costs £7.32, so we write this first:
№ of PENS COST
---------------------------
12 pens ► £7.32
Step 2: We want to find the cost of 9 pens, so we write 9 pens under the 12 pens:
№ of PENS COST
---------------------------
12 pens ► £7.32
9 pens ► _____
▲ ┌────────────────┐
└───────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { 9 }{ 12 }\) (i.e. the number at the bottom divided by the number at the top):
№ of PENS COST
---------------------------
┌ 12 pens ► £7.32
Χ 9 │
12 │
└► 9 pens ► _____
Step 4: The SAME Scale-factor (\(\times \frac { 9 }{ 12 }\)) will also convert the £7.32: № of PENS COST
---------------------------
┌ 12 pens ► £7.32 ─┐
Χ 9 │ │ Χ 9
12 │ │ 12
└► 9 pens ► _____ ◄┘
Step 5: So the answer is: \( £7.32\;\times\; \frac { \color{yellowgreen}{12} }{ \color{cornflowerblue}{9} } \;=\; \color{mediumvioletred}{£........} \)
But - REMEMBER - THAT'S NOT THE FINAL ANSWER: Remember, the mean and smelly shopkeeper is gonna charge us extra for breaking-the-pack. Fleabag!
Question 2: Stop crying! Okay - so you don't know nuffink about coulombs and joules - it doesn't matter... This is just about proportions, so it doesn't make any difference to us if we understand the rest of the jargon or not! Step 1: We know that 5 coulombs equates to 19 joules, so we write this first:
Coulombs Joules
------------------------------------
5 coulombs ► 19 joules
Step 2: We want to find the cost of 9 pens, so we write 9 pens under the 12 pens:
Coulombs Joules
------------------------------------
5 coulombs ► 19 Joules
6.5 coulombs ► ________
▲ ┌────────────────┐
└───────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { 9 }{ 12 }\) (i.e. the number at the bottom divided by the number at the top):
Coulombs Joules
------------------------------------
┌ 5 coulombs ► 19 Joules
Χ 9 │
12 │
└►6.5 coulombs ► ________
Step 4: The SAME Scale-factor (\(\times \frac { 9 }{ 12 }\)) will also convert the £7.32:
№ of PENS COST
-----------------------------------
┌ 5 coulombs ► 19 joules ─┐
Χ 9 │ │ Χ
12 │ │
└►6.5 coulombs ► ________ ◄┘ ▲ ║ This fraction is
└───────╢ the same as the
║ opposite fraction
Step 5: So the answer is....
Question 3: OUCH! Do you even know what a Chinese-burn (AKA: Chinese Wrist-burn ) is???
We can assume that the PRESSURE that we apply when giving a Chinese-burns is proportional to the VOLUME of the resulting SCREAM!!!
Pressure Volume
---------------------------
120 Pa ► 300 dB
▲ ║ that's the
└─────────╢ abbreviation
║ for decibels
Step 2: We want to find the cost of 4.75 kg, so we write 4.75 kg under the 2.5 kg:
Pressure Volume
---------------------------
120 Pa ► 300 dB
_____ ◄ 460 dB
▲ ┌───────────────┐
└────────┤ Make sure the │
│ UNITS LINE UP │
└───────────────┘
Step 3: The Scale-factor is: \(\times \frac { 460 }{ 300 }\) (i.e. the number at the bottom divided by the number at the top):
Pressure Volume
---------------------------
120 Pa ► 300 dB ─┐
│ Χ460
│ 300
_____ ◄ 460 dB ◄┘
Step 4: The SAME Scale-factor (\(\times \frac { 4.75 }{ 2.5 }\)) will also convert the £1.20:
Pressure Volume
---------------------------
┌─ 120 Pa ► 300 dB ─┐
Χ
│ │ Χ460
│ │ 300
└► _____ ◄ 460 dB ◄┘
Step 5: So the answer is: ...
Question 4: This is a slightly tricky question - because we have to figure out which ingredient is lacking (i.e. which ingredient is the limiting factor in making lemonade)... Perhaps we can start with a guess: Less imagine that the TONIC-WATER is the limiting ingredient: Then let's work out how much lemonade we can make with 2-litres of TONIC WATER: The recipe tells us that 375 ml of tonic water must be mixed with 3 lemons and 23 ml of maple syrup:
TONIC LEMONS SYRUP
--------------------------------------------
375 ml ► 3 № ► 25 ml
Step 2: We want to find the quantities to use with 2000 ml (2 litres) of TONIC WATER:
TONIC LEMONS SYRUP
--------------------------------------------
375 ml ► 3 № ► 25 ml
2000 ml ► ___ ► _____
▲ ┌────────────────┐
└────────────────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { 2000 }{ 375 }\) (i.e. the number at the bottom divided by the number at the top):
TONIC LEMONS SYRUP
--------------------------------------------
┌ 375 ml ► 3 № ► 25 ml
Χ2000 │
375 │
└►2000 ml ► ___ ► _____
Step 4: The SAME Scale-factor (\(\times \frac { 2000 }{ 375 }\)) will also convert the other values:
TONIC LEMONS SYRUP
--------------------------------------------
┌ 375 ml ► 3 № ─┐ ► 25 ml ─┐
Χ2000 │ │ Χ2000 │ Χ2000
375 │ │ 375 │ 375
└►2000 ml ► ___ ◄┘ ► _____ ◄┘
Step 5: So the answers are: \( 3\;\times\; \frac { \color{yellowgreen}{2000} }{ \color{cornflowerblue}{375} } \;=\; \color{mediumvioletred}{....} \) and \( 25\;ml\;\times\; \frac { \color{yellowgreen}{2000} }{ \color{cornflowerblue}{375} } \;=\; \color{mediumvioletred}{....\;ml} \) Looking at these numbers - it is clear that we got it WRONG - becuase we don't have 16 lemons, nor do we have 133⅓ ml of maple syrup... I'm not sure, but I think it was the LEMONS that are the limiting ingredient... So, we need to RE-CALCULATE, to see what we can make with a lousy 15 lemons:
LEMONS TONIC SYRUP
--------------------------------------------
3 № ► 375 ml ► 25 ml
Step 2: We want to find the quantities to use with 2000 ml (2 litres) of TONIC WATER:
LEMONS TONIC SYRUP
--------------------------------------------
3 № ► 375 ml ► 25 ml
15 № ► _____ ► _____
▲ ┌────────────────┐
└───────────────────────────────────────┤ Make sure the │
│ UNITS match up │
└────────────────┘
Step 3: The Scale-factor is: \(\times \frac { 15 }{ 3 }\) (i.e. the number at the bottom divided by the number at the top):
LEMONS TONIC SYRUP
--------------------------------------------
┌ 3 № ► 375 ml ► 25 ml
Χ15 │
3 │
└►15 № ► _____ ► _____
Step 4: The SAME Scale-factor (\(\times \frac { 15 }{ 3 }\)) will also convert the other values...
Question 5: If you use 60 minutes (instead of 1 hour) under the 12 minutes, you should have no-problem doing the calculation... But the end of the question asks you to think, "why is this poop?": In other words, why might this answer turn out be be very wrong? Well - if you knew you only had to do push-ups for 12 minutes, you might go a bit faster than if you had to do them for AN HOUR!!!
Question 6: I think you'll have no problem in working out how many DAYS it would take to pain the Forth Bridge... Once you've done that, you need to work out HOW MANY YEARS that equates to (given I'm only working 230 days per year)...
Question 7: Let's clear up the acronyms first: I.C.E. = Internal Combustion Engine (i.e. old fashioned petrol or diesel car) B.E.V. = Battery Electric Vehicle (i.e. a fully electric vehicle, with no engine - hybrid cars have a little engine - they don't count...) RANGE = Distance the vehicle can travel - in the case of a petrol car; on 1-full tank - in the case of an electric car; on a full charge. Note: Range isn't a big issue for ICE cars as it takes minutes to re-fill the tank at a petrol station. It is more of a concern with an electric car, as charging points are not widespread and even when you do find one, it takes hours to recharge.... So - let's start by working out the RANGE of my petrol car:
LITRES DISTANCE
------------------------------------
8 litres ► 124 km
54 litres ► _______
▲ ┌──────────────────┐
└────────┤ That's the RANGE │
│ of my I.C.E. car │
└──────────────────┘
Now, I require an electric car with at least ⅔ of that RANGE
Question 9: Don't be scared by the unfamiliar topics in this question, the working is just the same as before...
RESISTANCE VOLTAGE
-----------------------------------
5 Ω ► 6 V
2 Ω ► ____
An, in the same way, we can find \({ V }_{ PQ }\)
Question 10: I'm trying to confuse you (a bit, not too much) - but if you START by working out how many calories are in the the whole box (i.e. 540g), then it becomes just as easy as the previous questions...
Question 11: This is a NON-CALCULATOR QUESTION - make sure you show enough workings
|
|
THEN GO-COMPARE! |
Question 12, part (a):
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
Okay - they are getting a little trickier: This question has thrown Standard Index Form (SIF) into the mix - but again, this doesn't really cause us much in the way of problems...
Distance Cost
--------------------------------------
┌ 8Χ10⁷ km ► £2.5 million
Χ
│
│
└►6.4Χ10⁸ km ► ________
So, you need to divide (without using your calculator): \(\frac { 6.4 \;\times\; { 10 }^{ 8 } }{ 8 \;\times\; { 10 }^{ 7 } }\):
Don't let the SIF scare you ![]() :
:
6.40000000000 Χ 10⁸
8.000000000 Χ 10⁷ 64.0000000000 Χ 10⁷
80.00000000 Χ 10⁶ 640.000000000 Χ 10⁶
800.0000000 Χ 10⁵ 6400.00000000 Χ 10⁵
8000.000000 Χ 10⁴ 64000.0000000 Χ 10⁴
80000.00000 Χ 10³ 640000.000000 Χ 10³
800000.0000 Χ 10² 6400000.00000 Χ 10²
8000000.000 Χ 10Ή 64000000.0000 Χ 10Ή
80000000.00 Χ 10⁻⁰ 640000000.000 Χ 10⁻⁰
So, we are dividing:
cancel out the common 0s
6 4 0 0 0 0 0 0 0 =
8 0 0 0 0 0 0 0
cancel out the common 0s
Actually - there is a MUCH, MUCH QUICKER WAY: just make the exponents the same, then divide: \(\require{cancel}\)
\[\frac { 6.4\times { 10 }^{ 8 } }{ 8 \;\times\; { 10 }^{ 7 } } \;=\;\frac { 64 \; \cancel{\times\; { 10 }^{ 7 }} }{ 4 \; \cancel{\times\; { 10 }^{ 7 }} } \;=\;\frac { ... }{ ... }\]
Question 12, part (a):
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
Okay - let's work out how far we can get with £750 million:
Distance Cost
--------------------------------------
8 Χ 10⁷ Pa ► £2.5 million ─┐
│ Χ750
│ 2.5
_________ ◄ £750 million ◄┘
All that's left to do is to see which we can afford to travel to...
Question 14:
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
Again - we have a slight extra layer of complexity in this question - but it's not much; just testing to see if you can think!
Let's start off with the NORMAL setting:
TIME № of BOTTLES
------------------------------
6 hours ► 840 bottles
5 hours ► ___________
But - some will be under-filled, "on average 20 bottles per hour will be under-filled"
This is easy to figure out without any working, but if you want, you can use the Scale Factor Method to work out how many are under-filled (i.e. 1 hr ───►20 and 5 hrs ───►___ )...
Now l's do the FAST setting:
TIME № of BOTTLES
------------------------------
┌► ⅓ hours ► 58 bottles
│
│ 5 hours ► __________
everyone knows ─┘
20 mins = ⅓ hr
But - TWICE the rate of under-filling, "on average 2040 bottles per hour will be under-filled"
This is easy to figure out without any working, but if you want, you can use the Scale Factor Method to work out how many are under-filled (i.e. 1 hr ───►40 and 5 hrs ───►___ )...
Then: GO-COMPARE! ![]()
Question 15:
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
THREE-FOR-THE-PRICE-OF-TWO is a very popular supermarket offer. It means you can take three of these items and only pay for two. You can only do that if it says so. Otherwise it's called STEALING!
Anyway, if we take THREE of the SMALL bags, then well have a total of 18 kg of sprouts (?) and paid a total of £3.96
You might have noticed that £3.96 is exactly the same amount that it would cost you to buy \(\boxed { ??? }\) LARGE bags of sprouts (which are not on any offer)...
So you can compare how much sprouts you get if you spend £3.96 on SMALL bags, or if you spend £3.96 on LARGE bags
NOTE: While the method I've shown above is the easiest way to make the comparison (given it's a non-calculator question), the conventional way to make a comparison of different offers for the same goods is to do a RATE comparison (which means you work out the cost per kilogram for both the SMALL bags (on the offer) and for the LARGE BAGS...
Clue (for the last part): Your complaint should NOT be ANYTHING TO DO WITH CARROTS: You can't go into a shop that has sprouts on offer and then complain that carrots are not on offer - by that logic, if they put one-thing on offer, they'd have to put everything on offer!!! Come on, numpty!
Question 17, part (c):
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
What I'm hoping you'll notice here is:
YACHT MODEL
---------------------------------------
┌─────┐
mast: 180 cm ┤χ22.5├► 8 cm
└─────┘
┌─────┐
deck-length: 450 cm ┤χ22.5├► 20 cm
└─────┘
┌─────┐
deck-width: 270 cm ┤χ22.5├► 12 cm
└─────┘
┌─────┐
deck-area: 121500 cm ┤ NOT ├► 240 cm
│χ22.5│
└─────┘
Later on - this will become important: To realise that a Scale-factor that WORKS for lengths, WON'T WORK for areas/volumes
NOTE: If you are really alert, you'll have realised that \(121500\;cm\;\xrightarrow { \div { 22.5 }^{ 2 } } \;240\;cm\)
Question 18:
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
So there are two elements that make up the cost of the scaffolding:
1) The LABOUR cost of erecting/dismantling it: This is fixed regardless of how long you want it for
2) The HIRE of the scaffolding: This depends on how long you want it
We only apply the Scale Factor Method to the 2nd element...
So for this example: (1) LABOUR = £400 and (2) HIRE = £196 for 42-days
We need to adjust (2) for 36-days, then add back (1)...
Easy!
Question 19:
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
Again - I am trying to see if I can confuse you - and you MUSTN'T let me...
"At 60 km/h a car uses 15 litres to travel 164 km":
FUEL USED DIST TRAVELLED
--------------------------------
AT 60 KM/H 15 litres ► 164 km
"At 60 km/h TWICE THAT SPEED a car uses 15 litres to travel 164 km HALF THAT FAR":
FUEL USED DIST TRAVELLED
--------------------------------
AT 120 KM/H 15 litres ► 82 km
But this still doesn't help: we need to know what the RULE is for 90 KM/H???
Perhaps, if we look again:
FUEL USED DIST TRAVELLED
-------------------------------- ╖
AT 60 KM/H 15 litres ► 164 km ╟─────┐
AT 120 KM/H 15 litres ► 82 km ╟─────┤
--------------------------------------------------╜ ├──╢ AVERAGE THESE!
AT ___ KM/H 15 litres ► ___ km ◄─────┘
Then you're good to go...
Question 20:
This is a NON-CALCULATOR QUESTION - make sure you show enough workings
to convince me you did this without consulting your calculator...
In this question, you are combining your knowledge of APPROXIMATION with your knowledge of Scale Factor Method
What should we approximate 44985 grains as?
What should we approximate 0.0099976 as?
Question 21: The first thing you need to do is to calculate the cost of the amount of EACH ingredient she uses in the recipe:
So, to start with:
Mass Cost
---------------------------
BROWN SUGAR: 500 g ► £6.48
125 g ► _____
And you have to repeat that for every ingredient...
Once you've done that - you'll have the cost for making 4 date-squares. Divide it by 4 and subtract from £2.50 to work out the profit on each date-square...
Now the interesting bit: How many does she need to sell per day, so match her income from her job?
Well, she get £24,000 a year. There are 52 weeks in a year, but she gets 4-weeks off, so that's £24,000 for 48-weeks of work...
We need to figure out what that equates to PER DAY?
Then, we should be able to figure out how many date-squares she needs to sell per day.
NOTE: nWn means nearest whole number
Question 22: Again - we need to work out a comparison...
So again - there are two ways:
One way is to convert the annual salary offered to him into an hourly rate - then compare with his existing hourly rate...
The other way is to convert his existing hourly rate into a salary...
BOTH METHODS ARE AS GOOD AS EACH OTHER - so do whatever takes your fancy..
In either case - you need to work out how many hours the job entails: It's 7Ό hours-a-day, 5 days-a-week, 48 weeks-a-year
Why 48 weeks? THINK!
Question 23: Okay - these questions are getting quite convoluted now - a real test of your concentration:
Let's do this slowly, carefully and logically:
1) How many hours does she work each week?
First take the 48 minutes (lunch break) off the 8-hours
Remember, your calculator can help you convert 48 minutes into hours:
·
Press:
0
°"
48
°"
0
°"
=
.
Finally, press:
°"
once more
·
This is her lunch break (in hours), so take that away from the 8 hours she's at work and multiply by 5 to get her weekly hours of typing...
2) She has to write 12 reports-a-day = 60 letters-a-week: so let's first work out how long that takes (use Scale Factor Method) and then take that away from her weekly typing hours to work out how much time she has left for report writing...
3) Use the Scale Factor Method to work out how long a report takes to write in hours (use the average of the number of words!)
4) Finally, using (3) and (2) work out how many reports she can write. Then treat yourself to a cup of tea and an oreo biscuit (they are vegan)
Question 24: This is a NON-CALCULATOR QUESTION - so make sure you show enough workings to convince me you did this without consulting your calculator...
This is another question that combines APPROXIMATIONS with the Scale Factor Method
Approximate the volume of the car my multiplying 3.54 ≈ 3.5 m by 1.95 ≈ ....m by 1.49 ≈ ....m
We want the internal volume, which is 33.38% ≈ ⅓ of the external volume
Then use the Scale Factor Method starting with:
№ of skittles Volume
-----------------------------------------------
75 № ► 0.000118994 ≈ 1.2 Χ 10-4 m³
Question 25, part (a): This is a NON-CALCULATOR QUESTION - so make sure you show enough workings to convince me you did this without consulting your calculator...
This is another question that combines APPROXIMATIONS with the Scale Factor Method
Use the Scale Factor Method starting with:
№ sheets Thickness
-----------------------------------------
500 sheets ► 6.248 ≈ 6.25 cm
Question 25, part (b): Work out the area of 1 sheet of A4 paper (use ≈ 0.2 m by ≈ 0.3m) and then work out the mass of 1 sheet of A4 paper using the Scale Factor Method starting with:
Area Mass
---------------------------
1 m² ► 100 g
Question 26: You know this song, dontcha? If not follow this link:
We can do this in TWO stages:
1) Step 1: Decrease the number of woodchucks (keeping the time at 20 minutes):
№ woodchucks № wood
------------------------------------------
┌ 21 woodchucks (20 mins) ► 20 №
Χ12 │
21 │
└►12 woodchucks (20 mins) ► ____
2) Step 2: Increase the TIME (keeping the number of woodchucks at 12):
Time № wood
------------------------------------------
20 mins (12 woodchucks) ► 20 №
Question 29: This is another COMPARISON question:
This time it makes sense to compare the cost per 100g (or the cost per gram) of each:
1) At WAITROSE: You pay for two (£5), but you get three (975g), so the cost per 100 g is:
MASS COST
---------------------------
┌ 975 g ► £5.00
Χ100 │
975 │
└►100 g ► _____
2) At TESCO: You pay for 1½ (£...), but you get two (...g), so the cost per 100 g is:
3) Then:
|
THEN GO-COMPARE! |
Question 31: This is a bit tricky, because both the mass we are given (568 g and 200 g) don't refer to the tea - they refers to both the tea the the bottle. What we need is a volume of just tea to relate to a mss of just tea...
...the way to get that is to look at the DIFFERENCE between the two states: What was the change in volume of tea and the change in mass.
Then we can work out the mass of 568 ml of just tea...
...then we can find the mass of the empty bottle...
Question 32: This is similar to question 32, but one-notch up in difficulty again: That doesn't mean that you can't do it, it just means that you need to take it slow and break the problem down into simple steps...
If you start with the cluster of stacked trolleys, like this:

Then you'll be too confused to work out what is going on...
So, you need to take it slowly - start with JUST ONE TROLLEY:
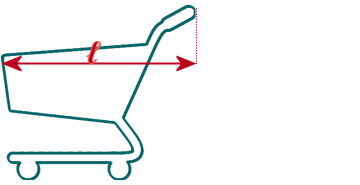
You can see that I've marked its length as \(l\)
If we have two trolley, but we don't STACK them, then:
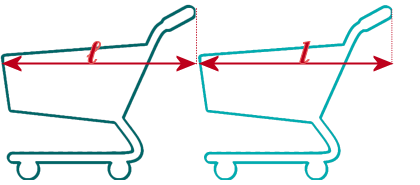
The total length would be \(2l\)
But, of course, we could stack them:
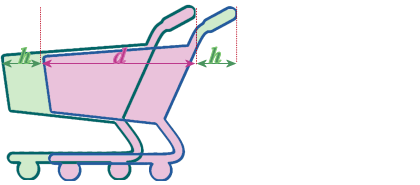
I've labelled the bit that overlaps as \(d\)
I've also labelled the two bits that DON'T OVERLAP: The bit that sticks out from the front of the 1st trolley, I've labelled that as \(h\). The bit that sticks out from the back of the 2nd trolley, I've labelled that also as \(h\). WHY?
Finally, I noticed that the TOTAL LENGTH of the two trolleys is:
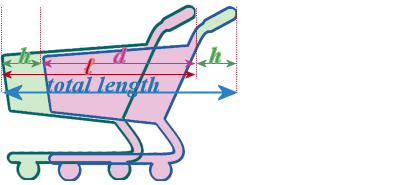
So, the total length of TWO TROLLEYS = length of 1-trolley + the amount that the 2nd doesn't all the way in by...
Okay = good. We figured something out!
Let's now look the situation for 2 trolleys...
And 4...
Etc...
Eventually, you might realise that this question as actually analogous to Q 31 - with the bottle of green tea...

