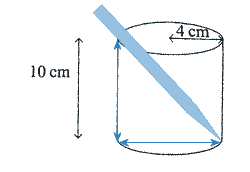
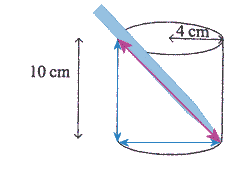
G.C.S.E. Jun 2003 - Paper 6Question 1, part (b): They are trying to say that, if the pencil rests 'diagonally' in the cylinder, will it fit?
So, you need to work out the length of the diagonal of the cylinder...
Question 2, part (b): The "highest common factor" is the largest number that goes into both. We have already found the prime factors of each... Taking only the prime factors they "have in common"
(they have 2² and ... in common) and multiplying those
together... Question 2, part (c): The "lowest common multiple" is the smallest number that both of these will go into You find this by multiplying all of the prime factors together, crossing out any that are repeats. Since 2² is in both and 3 is in both, we cross the repeats of these out: LCM = (2² Χ 3) Χ (
Question 3, part (a): First of all, write out a new table using the "upper boundaries" of each class and the cumulative frequencies...
n = 40 The median is the: (½n + ½)th value = 20½th value Since we can't find 20½ in the 'F' values:
▲ ║ ╒════════════════════╩════════════════════════╕ we look in the 'F' values for the number that is just GREATER than 20½, which is: 29 ╘═════════════════════════════════════════════╛ This comes from the class whose U.C.B. is: 200 Which means the: ... < C ≤
200 class Question 3, part (b): All that would happen is that we would add another class that the end of the table (perhaps 0<C≤1000) and then n would be 41, so the median would be the ...th value - which would still be in the same class... So the answer is "NO!" and you should remember that
the mean is affected by one or two extreme values but the median
ISN'T Question 3, part (c): So, £5200 is 80% of the original amount...
Question 4, part (a): So, the height is (x+1) Which means the volume is: ... Χ ... Χ ... And since this equals 230... Question 4, part (b): Re-writing the equation to make one side = 0 x³ + x² - 230 = 0 ╚═════f(x)═════╝ We need to put in two values, where one gives a negative answer and the other gives a positive answer: Try: f(5) = (5)³ + (5)² - 230 = -80 (which is a negative answer) Try: f(6) = (6)³ + (6)² - 230 = 22 (which is a positive answer) The change in sign does show the root must lie between x=5 & x=6 Try: f(5.5) = ... (which is negative) ◄ So '5.5' replaces '5' in our ROOT INTERVAL because x=5 gave a negative answer last time So, now we know the root lies between x=5.5 & x=6 Try: f(5.8) = ... (which is negative) ◄ So '5.8' replaces '5.5' in our ROOT INTERVAL because x=5.5 gave a negative answer last time So now we know the root lies between x=... and x=6 Try: f(5.9) = ... (which is positive) ◄ So '5.9' replaces '6' in our ROOT INTERVAL because x=6 gave a positive answer last time So, now we know the root lies between x=5.8 & x=5.9 Now, we have to pick one of these as our solution The answer when we put in x=5.8 was closer to zero...
Question 6, part (b): They want ANY equation which is parallel to: y = ½x + 1 There are loads - any equation which also has a gradient of ½: y = ½x + ...
Question 8, part (a): This is the topic, "similar triangles" (the proof that they are similar is easy, but I wont go into it here) Draw out triangle ABE Now draw out separately, triangle ACD:
You know the length AE = 6 cm and the corresponding length on the BIG triangle is 10 cm So, the scale factor is 10/6 We can use this to multiply the length BE by, in order to get the length CD...
Question 9: Firstly, lets do 'a Χ b': When multiplying, multiply the numbers and add the powers... ┌┬┐
╒╧╕ ╒╧╕ │
a Χ b = 3 Χ 108 Χ 2 Χ 107 │
╘╤╛ ╘╤╛ │
└┬┘ │
= ... Χ 1015 │
└┘
Next, lets do 'a + b': When adding, write the numbers so the powers are the same first (change the one with the smaller power by increasing its power by '1' for each place you move the decimal back) 0 2.0 Χ 107 = 0.2.0 Χ 10 └┘ ▲ move the decimal │ back 1 place └ and increase the power by '1' And, once the powers are the same, simply add the numbers and use the same power: ┌┬┐
╒╧╕ ╒╧╕ │
a + b = 3 Χ 108 + 0.2 Χ 108 │
╘╤╛ ╘═╤═╛ │
└┬┘ │
= ... Χ 108 │
└┘
Finally, to divide these two answers, we divide the numbers and subtract the powers: ab = 30 Χ 10
a + b
Now - this is the answer, but it is NOT in standard from. We need to move the decimal back one place, which means we must i---ea-e the power by 1
Question 11, part (b): I think we only need to consider the outcomes, '6' and 'not 6' So, the branches for the 1st event (i.e. the red die) are '6' and 'not 6' and the probabilities are ... and ... And the branches for the 2nd event (i.e. the blue die) are again, '6' and 'not 6' ...
Question 12, part (a): Stick A & B together to form a large cone... Work out the volume of the large cone (remember, V = 1/3 лr²h) Then work out the volume of the small cone A Subtract these to find the volume of the frustrum... Question 12, part (b): h -----> sqr -----> +d² -----> √ -----> Χ2лd So, firstly, divide by 2лd Question 12, part (c): This is the topic, "similar shapes" Draw the small frustrum Now, beside that, draw the large frustrum:
The height of the small frustrum is 20 cm and the height of the large frustrum is 30 cm. So, the length scale factor is 30/20 So, the length scale factor is: SMALL BIG ---------------------------- 20 cm ► 30 cm χ10 χ10 ---------------------------- 2 cm ► 3 cm
But, we need the area scale factor: SMALL BIG ----------------------------- l.s.f 2 cm ► 3 cm sqr sqr ----------------------------- a.s.f. 4 cm² ► 9 cm² We know the area of the small frustrum is 450 cm²: SMALL BIG ----------------------------- 4 cm² ► 9 cm² 450 cm² ► ... Question 13, part (a): Remember the area of a trapezium is: A = ½h (a + b) Where a and b are the parallel sides and h is the distance
between them... Question 13, part (b): I'm gonna use 'completing the square' to solve this: x² + 20x = 400 ║χ2 ╠══════╗ (x + 10)² - 10² = 400 (x + 10)² - 100 = 400 + 100 +100 ---------------------- (x + 10)² = 500 √ √ -------------------------------------- x + 10 = ... or -22.3607 Etc...
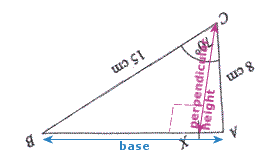
Question 14, part (a): Remember the second equation for the area of a triangle: A = ½ab sin C Where C is the angle between the sides a and b Question 14, part (b): If you turn your head on its side (no - better still, just turn the paper around) so that AB is now the BASE of triangle ABC:
Then, CX would be the height (since it is at 90° to AB): A = ½ Χ base Χ height And we already know from part (a) that the area of this triangle is ... A = ½ Χ base Χ height ... = ½ Χ AB Χ h . . . . . eqn (1) So, if we work out the base (AB) and plug it into equation (1), then we'll be able to solve it to find b So first, we have to find the length AB (cosine rule): |AB|² = 8² + 15² - 2(8)(15) cos 70 => |AB|² = ... => |AB| = ... And plug this into equation (1)... Question 15, part (b): In part (a), you learned that: (2a-1)² - (2b-1)² = ... Now, '2a' represents an even number (since any whole number multiplied by 2 gives an even number) So, '2a-1' represents an odd number (1 less than any even number is always an odd number) And '2b-1' represents another odd number So: (2a-1)² - (2b-1)² represents the difference between the squares of any two odd numbers. Now, we showed that this is equal to: 4(a-b)(a+b-1) Which proves that 4 is a factor, but they want us to show that 8 is a factor!!! So, we need to show that '2' is a factor of: (a-b)(a+b-1) Well that's easy to show: There are only two possibilities: Q.E.D. (that stands for "Quad Erratus Demonstratus" - the proof is demonstrated)
Question 16, part (a): Start by finding the L.B. and U.B. of each of the numbers: TL.B. = ... TU.B. = 1.35 LL.B. = 4.495 LU.B. = ... xL.B. = 29.5 xU.B. = ... To find the lower bound for 'g': ╒═══════════════╕ occurs when
│ The L.B. of g ├┐
╘═════╤═════════╛ │
▼ U.B. │
g = 2L ◄┼ The top of the fraction is smallest
T² sin x ◄┴ The bottom of the fraction is largest
L.B.
2LL.B.
g =
(TU.B.)² sin (xU.B.)
g = 2(4.495) = ....
(...)² sin (...)
Similarly, To find the upper bound for 'g': ╒═══════════════╕ occurs when
│ The U.B. of g ├┐
╘═════╤═════════╛ │
▼ U.B. │
g = 2L ◄┼ The top of the fraction is largest
T² sin x ◄┴ The bottom of the fraction is smallest
L.B.
Etc... Question 16, part (b): Are our answers for the L.B. and U.B. of g THE SAME? No? What if you round them both to 3 s.f. - then do they give the same value? Still No? What if you round them both to 2 s.f? Still No? What if you round them both to 1 s.f? Yes? Then that is the accuracy that you can give 'g' to...
Question 17, part (a): Using the rules of indices: which is 'x' ╗ ╔ which is 'y' ╒╩╕ ╒╩╕ 2p+q can be written as 2p Χ 2 22q can be written as (2q) ╘╦╛ ╚ which is 'y' 2p-1 can be written as 2p Χ 2-1 = 2p Χ ... = ½(...) ╘╦╛ ╚ which is 'x' Question 17, part (b): You probably just want to solve the simultaneous equations as normal (make x the subject of equation (1), sub it into (2) and solve...) But, what they are getting at is this use of powers of '2'... 32 can be written as 25 We know from above that xy = 2p+q We can deduce that 2xy² = 2(2p)(2q)² = 21+p+2q So: 2p+q = 25 => p + q = 5 21+p+2q = 25 => 1 + p + 2q = 5 Etc...
Question 18: This is a 'complete the square' question: If you have: x² - 2mx And you complete the square: (x - m)² - m² But they got: (x - m)² - k Which means that: m² = ... Note: The 'easier' way to do this
question is just to expand the R.H.S. and then simplify - but
you don't learn as much doing it that way... Question 18, part (b): The completed square makes it easy for us to find the minimum value... For example: (x - 3)² - 20 So, for their equation ...
Question 19: A and B are independent if p(A and B) = p(A) Χ p(B)
Question 20: What have they done to the COS graph?
Well clearly they've reflected it in the x-axis
And then they've squashed it by 4 along the x-axis (because 1 cycle of their graph is from 0° to 90°)
Then they've stretched it by ... (so far out graph has a total ht of '2', whereas theirs has a total height of '100') And then they've shifted it up by ... So the flow diagram is: ╒═════════════════════╕ ║ ╒══════════════════════╕
inside the brackets ║ outside the brackets
╘══════════╤══════════╛ ║ ╘═══════════╤══════════╛
╒═══╧═══╕ ╨ ╒═════════════════╧═════════════════╕
x ► Χ4 ► COS ► Χ
► Χ-1 ► +
So, the equation is: y = -...cos(4x) + ... Note: For y = a - b cos (kt) or y = a +
b cos (kt) |